LC – автогенератор на операционном усилителе

На рис.4.2 представлена схема генератора на операционном усилителе. Цепь обратной связи представляет собой колебательный контур. Коэффициент усиления определяется цепью отрицательной обратной связи, включенной на инвертирующий вход. Резистор R отделяет низкоомный выход операционного усилителя от контура. При условии, что R >> R₁, его можно считать включенным параллельно контуру. Напряжение обратной связи u(t) снимается с контура и подается на неинвертирующий вход операционного усилителя. В силу виртуальной замкнутости входов усилителя

U_вых(t) = Ku(t).

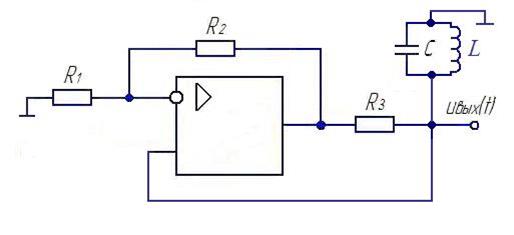
Рис.4.2. LC-генератор на операционном усилителе

Ток, подтекающий к узлу A, определяется разностью потенциалов на R и равен [(K-1)u(t)]/R. Для узла A закон Кирхгофа дает

.

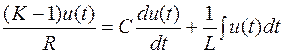Продифференцировав обе части уравнения, получим

.

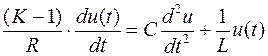Введем обозначения: 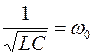- резонансная частота контура, 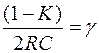- коэффициент затухания.

После несложных преобразований получим

.

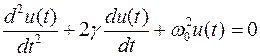Найдем корни характеристического уравнения s² + 2gs+w₀² = 0

.

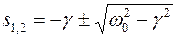Решение дифференциального уравнения при нулевых начальных условиях имеет следующий вид

.

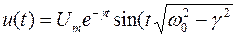Форма колебаний при g<0 или K>1 будет носить нарастающий по амплитуде характер. Случай g=0 или K<1 исключен в данной схеме. При g=0 или K=1 на выходе генератора будет действовать гармонический сигнал u(t) = U_msinw₀t. Этот случай отвечает балансу амплитуд и фаз. В рассматриваемом случае все напряжение с колебательного контура поступает на вход операционного усилителя, т.е. K_ос = 1. Тогда KK_ос = 1, что соответствует балансу амплитуд. Уравнение баланса фаз также выполняется, так как на резонансной частоте контур эквивалентен активному сопротивлению и полный фазовый сдвиг в цепи обратной связи и операционного усилителя равен нулю.

Таким образом, рассмотренная схема представляет собой пример автогенератора гармонического колебания. Для самовозбуждения потребуется выполнить схему с коэффициентом усиления, несколько большим единицы, с последующим снижением до значения K=1 за счет нелинейности усилительной характеристики операционного усилителя.