ЗАКОНЫ ОМА И КИРХГОФА В ОПЕРАТОРНОЙ ФОРМЕ

Выделим в некоторой сложной цепи ветвь ab (рис.1.18)

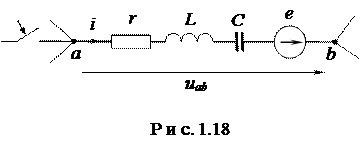Замыкание ключа во внешней цепи приводит к возникновению переходного процесса, при этом начальные условия для тока в ветви и напряжения на конденсаторе в общем случае ненулевые.

Для мгновенных значений можно записать:

.

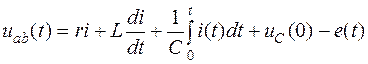Тогда на основании приведенных выше соотношений для операторных изображений получим:

.

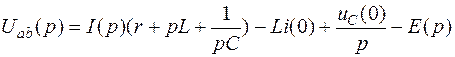Отсюда

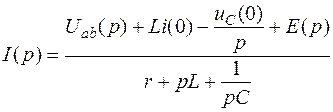
Обозначим 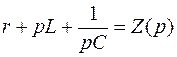- операторное сопротивление рассматриваемого участка цепи. Отметим, что операторное сопротивление 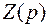соответствует комплексному сопротивлению 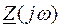в цепи синусоидального тока при замене оператора р на jω.

Получаем

.

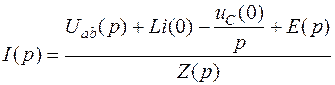Полученное уравнение есть математическая запись закона Ома для участка цепи с источником ЭДС в операторной форме.

В соответствии с ним для ветви на рис.1.18 можно изобразить операторную схему замещения(рис.1.19).

Величины Li(0) (направлена по току) и 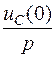(направлена против тока) называются внутренними (добавочными) ЭДС.

Величина внутренней ЭДС Li(0) обусловлена запасом энергии в магнитном поле катушки индуктивности при протекании по ней тока i(0) ≠ 0 непосредственно до коммутации. Величина внутренней ЭДС 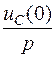обусловлена запасом энергии в электрическом поле конденсатора при наличии на нем напряжения u_C (0) ≠ 0 непосредственно до коммутации.

В частном случае, когда в ветви ab нет ЭДС e и к моменту коммутации i(0) = 0 и u_C (0) = 0 (нулевые начальные условия), закон Ома в операторной форме принимает более простой вид:

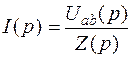
Сформулируем законы Кирхгофа в операторной форме:

Первый закон: алгебраическая сумма операторных изображений токов, сходящихся в узле, равна нулю

.

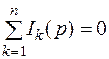Второй закон: алгебраическая сумма операторных изображений напряжений на пассивных элементах в контуре равна алгебраической сумме операторных изображений ЭДС, действующих в этом контуре

.

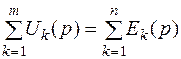Ненулевые начальные условия учитываются введением в уравнения внутренних ЭДС. С их учетом второй закон Кирхгофа принимает вид

.

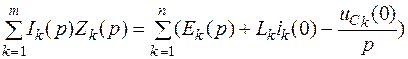Все основанные на законах Кирхгофа приемы и методы составления уравнений (методы контурных токов, узловых напряжений, эквивалентного генератора, наложения и т.п.) можно применять и при составлении уравнений для изображений