СО СТАЛЬНЫМ СЕРДЕЧНИКОМ

Рассмотрим процессы в катушке с числом витков w, расположенной на замкнутом ферромагнитном сердечнике (рис.2.13). Такую катушку можно представить частью некоторого электротехнического устройства.

Если обмотка включена в сеть переменного тока, то по ней будет протекать переменный ток, который создаст основной магнитный поток Ф₀ и поток рассеяния Ф_S. Основной магнитный поток Ф₀ проходит по ферромагнитному сердечнику и сцепляется со всеми w витками катушки, а поток рассеяния Ф_S основную часть пути проходит по воздуху и сцепляется только с частью витков обмотки.

Уравнение, описывающее процесс в такой катушке, имеет вид:

,

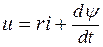где r – сопротивление проводов обмотки.

Полное потокосцепление 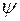можно представить в виде суммы двух составляющих

.

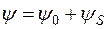Величина 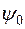есть потокосцепление, определяемое основным магнитным потоком, и может быть представлена в виде:

.

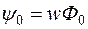Величина 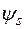есть потокосцепление, определяемое магнитным потоком рассеяния и определяется в виде

,

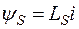где 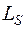- индуктивность катушки, обусловленная потоком рассеяния.

Так как магнитный поток рассеяния Ф_S основную часть пути проходит по воздуху – среде с линейными магнитными свойствами, то индуктивность 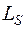можно считать независящей от тока и постоянной.

Потокосцепление ψ нелинейно связано с током, т.к. зависит от степени насыщения ферромагнитного сердечника.

С учетом этого уравнение катушки со стальным сердечником можно переписать в виде

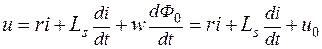(2.6)

Это уравнение нелинейное. Поэтому, даже если напряжение сети u синусоидально, то ток i в цепи будет несинусоидальным. Заменяя несинусоидальные ток и поток эквивалентными синусоидами, уравнение (2.6) можно записать в символической форме

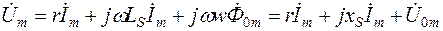(2.7)

Если считать основной магнитный поток синусоидальным

,

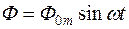то, применяя символический метод расчета, получим

.

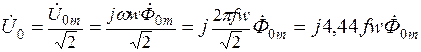Таким образом, получаем

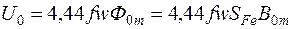, (2.8)

где 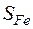- поперечное сечение магнитопровода.

Уравнение (2.8) часто называют уравнением трансформаторной ЭДС, которое широко применяется при расчете электромагнитных устройств.