ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
В основе работы большого числа электрических машин и аппаратов, например, генераторов, электродвигателей, трансформаторов и т.п., лежит закон электромагнитной индукции (закон Фарадея).
Электрический ток, протекая по проводнику, создает вокруг него магнитное поле. Это поле характеризуется индукционным и силовым действием.
Индукционное действие магнитного поля заключается в том, что если в магнитном поле движется проводник (рамка), то в нем индуктируется ЭДС. На этом основан принцип работы генераторов.
Силовое действие магнитного поля заключается в том, что на проводник с током и на ферромагнитные тела, находящиеся в магнитном поле, действуют электромагнитные силы. Это свойство магнитного поля лежит в основе принципа действия электродвигателей, электромагнитов и многих других электротехнических устройств. В большинстве случаев магнитное поле возбуждается токами, протекающими по обмоткам электротехнических устройств, реже – постоянными магнитами.
При решении электротехнических задач все вещества по магнитным свойствам подразделяются на две основные группы: неферромагнитные (диамагнитные, парамагнитные) и ферромагнитные [1,2,3]. Это разделение определяется значением относительной магнитной проницаемости 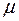 . Диамагнетики и парамагнетики имеют
. Диамагнетики и парамагнетики имеют 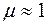 , а у ферромагнетиков
, а у ферромагнетиков 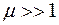 .
.
Для концентрации магнитного поля и придания ему желаемой конфигурации активные части электротехнических устройств, называемые магнитопроводами или сердечниками, выполняются из ферромагнитных материалов.
Магнитное сопротивление 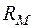 ферромагнитного сердечника определяется по формуле:
ферромагнитного сердечника определяется по формуле:
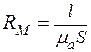 ,
,
где l - длина средней магнитной силовой линии, (м);
S – площадь поперечного сечения сердечника, (м2);
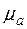 - абсолютная магнитная проницаемость сердечника, (Гн/м).
- абсолютная магнитная проницаемость сердечника, (Гн/м).
Путем несложных преобразований можно показать, что при равных геометрических размерах магнитное сопротивление воздуха (воздушного зазора) в 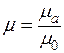 раз больше магнитного сопротивления ферромагнитного сердечника. Здесь
раз больше магнитного сопротивления ферромагнитного сердечника. Здесь 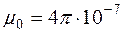 Гн/м – магнитная постоянная.
Гн/м – магнитная постоянная.
Таким образом, ферромагнитный сердечник служит для создания пути с наименьшим сопротивлением для прохождения магнитного потока.
Этим обеспечивается наибольший коэффициент магнитной связи между отдельными обмотками электротехнического устройства (трансформатора, электродвигателя и т.д.), т.е. наибольшая взаимная индуктивность M. Электрическая энергия из одной обмотки в другую переносится посредством магнитного потока Ф, следовательно, в конечном счете, увеличивается КПД установки.
2.1.2. ОСНОВНЫЕ ВЕЛИЧИНЫ, ХАРАКТЕРИЗУЮЩИЕ
ПРОЦЕССЫ В МАГНИТНЫХ ЦЕПЯХ
Основными векторными величинами, характеризующими магнитное поле, являются магнитная индукция 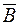 , намагниченность
, намагниченность 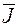 и напряженность магнитного поля
и напряженность магнитного поля 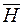 , связанные соотношением
, связанные соотношением
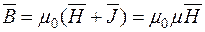 .
.
Магнитная индукция 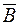 характеризует силовое воздействие магнитного поля на проводник с током.
характеризует силовое воздействие магнитного поля на проводник с током.
Намагниченность 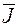 совпадает по направлению с вектором
совпадает по направлению с вектором 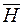 в данной точке и является магнитным моментом единицы вещества.
в данной точке и является магнитным моментом единицы вещества.
При расчетах магнитных цепей обычно используют две величины – магнитную индукцию 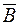 и напряженность магнитного поля
и напряженность магнитного поля 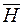 . При необходимости значение
. При необходимости значение 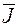 можно найти по соответствующим значениям
можно найти по соответствующим значениям 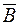 и
и 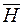 .
.
Основными скалярными величинами, характеризующими магнитную цепь, являются магнитный поток Ф, магнитодвижущая сила (МДС) F и магнитное напряжение UМ.
Величиной, служащей для интегральной оценки магнитного поля, является магнитный поток Ф, представляющий собой поток вектора магнитной индукции 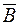 сквозь поперечное сечение магнитопровода S:
сквозь поперечное сечение магнитопровода S:
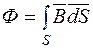 .
.
В случае, когда магнитный поток перпендикулярен сечению, через которое он проходит, получим:
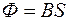 или
или 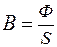 ,
,
т.е. магнитная индукция в этом случае равна магнитному потоку, проходящему через единицу площади поперечного сечения магнитопровода.
Магнитодвижущая (намагничивающая) сила F равна произведению тока I, протекающего по обмотке, на число ее витков w
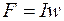 .
.
Положительное направление МДС совпадает с движением правого винта, если его вращать по направлению тока в обмотке. Можно сказать, что МДС вызывает магнитный поток в магнитной цепи подобно тому, как ЭДС вызывает электрический ток в электрической цепи.
Применение ферромагнитных сердечников позволяет получить намного бóльший магнитный поток при том же значении МДС.
Магнитное напряжение  на участке ab магнитной цепи равно линейному интегралу от напряженности магнитного поля между этими точками
на участке ab магнитной цепи равно линейному интегралу от напряженности магнитного поля между этими точками
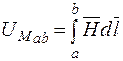 .
.
На практике на участках магнитных цепей напряженность 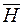 , как правило, постоянна и совпадает по направлению с вектором
, как правило, постоянна и совпадает по направлению с вектором 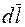 , поэтому
, поэтому
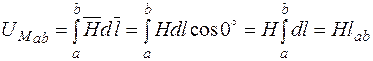 ,
,
где lab – длина участка магнитной цепи между точками a и b.
Важную роль при расчетах магнитных цепей играют вебер-амперные характеристики. Под вебер-амперной характеристикой участка магнитной цепи понимают зависимость проходящего по нему магнитного потока Ф от падения магнитного напряжения на этом участке
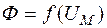 .
.
Отметим, что использование вебер-амперных характеристик во многом аналогично использованию вольт-амперных характеристик элементов при расчетах нелинейных электрических цепей [1,2], с той лишь разницей, что вебер-амперные характеристики изначально не задаются, а их необходимо построить с учетом геометрических размеров участков магнитной цепи и свойств материала сердечника.
2.1.3. ХАРАКТЕРИСТИКИ ФЕРРОМАГНИТНЫХ МАТЕРИАЛОВ
Ферромагнитные материалы состоят из областей самопроизвольного намагничивания (доменов). В ненамагниченном состоянии вещества векторы намагниченности отдельных областей направлены в различные стороны, поэтому намагниченность ферромагнитного тела не проявляется, если оно не помещено во внешнее магнитное поле.
Если же ферромагнитный материал поместить во внешнее магнитное поле, под его действием векторы намагниченности отдельных областей будут ориентироваться по внешнему полю.
В результате этого индукция результирующего магнитного поля оказывается во много раз (сотни и тысячи раз) больше, чем магнитная индукция внешнего поля до помещения в него ферромагнитного материала.
Свойства ферромагнитных материалов характеризуются зависимостью магнитной индукции B от напряженности магнитного поля H. При этом различают кривые намагничивания, представляющие собой однозначные зависимости, и гистерезисные петли - неоднозначные зависимости
Известно, что ферромагнитным материалам присуще явление магнитного гистерезиса – отставание изменения магнитной индукции 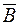 от изменения напряженности магнитного поля
от изменения напряженности магнитного поля 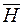 (рис.2.1)
(рис.2.1)
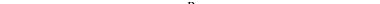
Гистерезис объясняется внутренним трением областей самопроизвольного намагничивания (явлением магнитной вязкости).
Кривая, проведенная через вершины частных циклов петель гистерезиса называется основной кривой намагничивания (ОКН). Аналитически она выражается формулой:
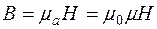 .
.
Основная кривая намагничивания является паспортной характеристикой ферромагнитного материала. Она может быть снята экспериментально или задана в справочниках.
Значение магнитной индукции 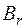 при напряженности
при напряженности 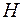 , равной нулю, называется остаточной индукцией (см. рис.2.1). Она определяет остаточный магнитный поток
, равной нулю, называется остаточной индукцией (см. рис.2.1). Она определяет остаточный магнитный поток 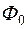 машины, который может долго сохраняться в ранее намагниченном сердечнике. На этом свойстве ферромагнитных материалов основан принцип работы электрических машин с самовозбуждением.
машины, который может долго сохраняться в ранее намагниченном сердечнике. На этом свойстве ферромагнитных материалов основан принцип работы электрических машин с самовозбуждением.
Напряженность магнитного поля 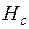 при индукции
при индукции 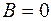 называется коэрцитивной (задерживающей) силой. Такая напряженность магнитного поля необходима для доведения магнитной индукции в предварительно намагниченном ферромагнетике до нуля.
называется коэрцитивной (задерживающей) силой. Такая напряженность магнитного поля необходима для доведения магнитной индукции в предварительно намагниченном ферромагнетике до нуля.
В общем случае ОКН является резко нелинейной характеристикой. Это накладывает определенные условия на работу аппаратов с ферромагнитными сердечниками.
Если рабочая индукция лежит в линейной области ОКН, то связь между током и напряжением является линейной, т.е. при синусоидальном поданном напряжении, ток в цепи так же синусоидален и наоборот.
Если рабочая индукция лежит в нелинейной области ОКН (насыщающийся участок), то электротехническое устройство будет описываться нелинейными уравнениями и при синусоидальном напряжении ток в цепи будет несинусоидальным, т.е. в нем появятся высшие гармоники. Это существенно усложняет расчет цепи и приводит к некоторым особенностям работы электрической машины или аппарата.
Перемагничивание ферромагнитного материала связано с расходом энергии на этот процесс. Площадь петли гистерезиса характеризует энергию, выделяемую в единице объема ферромагнетика за один период изменения магнитной напряженности (один цикл перемагничивания). В зависимости от величины этих потерь и, соответственно, формы петли гистерезиса ферромагнитные материалы подразделяются на магнитомягкие и магнитотвердые. Первые характеризуются относительно узкой петлей гистерезиса и круто поднимающейся основной кривой намагничивания; вторые обладают большой площадью гистерезисной петли и полого поднимающейся основной кривой намагничивания.
Магнитомягкие материалы (электротехнические стали, железоникелевые сплавы, ферриты) определяют малые потери в сердечнике и применяются в устройствах, предназначенных для работы при переменных магнитных потоках (трансформаторы, электродвигатели и др.). Магнитотвердые материалы (углеродистые стали, вольфрамовые сплавы и др.) используются для изготовления постоянных магнитов.
2.1.4. ОСНОВНЫЕ ЗАКОНЫ МАГНИТНЫХ ЦЕПЕЙ
В основе расчета магнитных цепей лежат два закона:
1. Закон (принцип) непрерывности магнитного потока, который формулируется следующим образом: поток вектора магнитной индукции через замкнутую поверхность равен нулю
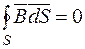 .
.
2. Закон полного тока, который формулируется следующим образом: циркуляция вектора напряженности вдоль произвольного контура равна алгебраической сумме токов, охватываемых этим контуром
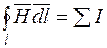 . (2.1)
. (2.1)
Как следует из первого уравнения Максвелла [1,2,3], линейный интеграл напряженности магнитного поля по замкнутому контуру есть мера электрического тока, проходящего сквозь поверхность, ограниченную этим контуром. Здесь под величиной тока подразумевают не только ток проводимости, но и ток переноса, а также и ток смещения сквозь эту поверхность. Сумма токов проводимости, переноса и смещения может быть названа полным током сквозь рассматриваемую поверхность. Поэтому соотношение (2.1) именуют законом полного тока.
Положительное направление интегрирования 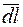 связано с положительным направлением тока I правилом правого винта.
связано с положительным направлением тока I правилом правого винта.
Например, если рассмотреть магнитное поле одиночного проводника, по которому протекает ток I, то получим выражение напряженности магнитного поля в точке, отстоящей на расстоянии r от оси проводника, в виде:
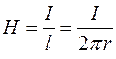 ,
,
где 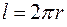 - длина окружности радиуса r.
- длина окружности радиуса r.
Если магнитное поле создается катушкой с числом витков w, по которым протекает ток I, то напряженность магнитного поля будет:
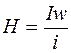 или
или 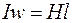 .
.
При анализе магнитных цепей обычно используют следующие допущения:
- напряженность магнитного поля и, соответственно, магнитная индукция во всех точках поперечного сечения магнитопровода одинаковы
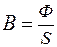 ;
;
- магнитный поток через любое сечение неразветвленной части магнитопровода одинаков (потоки рассеяния отсутствуют);
- сечение воздушного зазора равно сечению прилегающих участков магнитопровода.
Это позволяет использовать при расчетах законы Кирхгофа и Ома для магнитных цепей, вытекающие из законов, сформулированных ранее.
Первый закон Кирхгофа: алгебраическая сумма магнитных потоков в любом узле магнитной цепи равна нулю
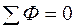 .
.
Первый закон Кирхгофа следует из принципа непрерывности магнитного потока.
Второй закон Кирхгофа: алгебраическая сумма падений магнитного напряжения вдоль любого замкнутого контура равна алгебраической сумме МДС вдоль этого же контура:
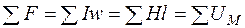 .
.
Второй закон Кирхгофа есть форма записи закона полного тока.
Рассмотрим падение магнитного напряжения 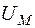 на участке магнитной цепи длиной l и сечением S:
на участке магнитной цепи длиной l и сечением S:
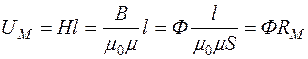 .
.
Закон Ома для магнитных цепей: падение магнитного напряжения на участке магнитной цепи равно произведению магнитного потока, проходящего по этому участку, и магнитного сопротивления RМ этого участка:
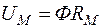 .
.
Сформулированные законы и понятия магнитных цепей позволяют провести формальную аналогию между основными величинами и законами, соответствующими электрическим и магнитным цепям.
2.1.5. АНАЛОГИЯ ВЕЛИЧИН И ЗАКОНОВ ДЛЯ ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ЦЕПЕЙ
Между электрическими и магнитными цепями существует формальная аналогия, основные соотношения которой представлены в таблице 2.1. Там же приведены размерности рассматриваемых величин в системе СИ.
Таблица 2.1
| Электрическая цепь | Магнитная цепь | ||||
| Параметр | Обозначение (формула) | Размерность | Параметр | Обозначение (формула) | Размерность |
| Удельное электрическое сопротивление | 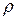
| Ом∙м | Удельное магнитное сопротивление | 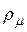
| м/Гн |
| Удельная электрическая проводимость | 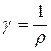
| См/м | Абсолютная магнитная проницаемость | 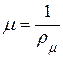
| Гн/м |
| Электрическое сопротивление | 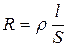
| Ом | Магнитное сопротивление | 
| 1/Гн |
| Электрическая проводимость | 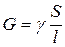
| 1/Ом | Магнитная проводимость | 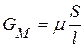
| Гн |
| Плотность тока | 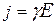
| А/м2 | Магнитная индукция | 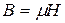
| Тл |
| Ток | 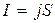
| А | Магнитный поток | 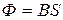
| Вб |
| Напряженность электрического поля | Е | В/м | Напряженность магнитного поля | Н | А/м |
| Напряжение | 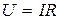
| В | Магнитное напряжение | 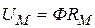
| А |
| Электродвижущая сила (ЭДС) | Е | В | Магнитодвижущая сила (МДС) | F | А |
| Закон Ома | 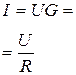
| А | Закон Ома | 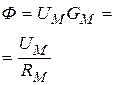
| Вб |
| Первый закон Кирхгофа | 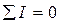
| А | Первый закон Кирхгофа | 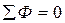
| Вб |
| Второй закон Кирхгофа | 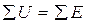
| В | Второй закон Кирхгофа | 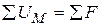
| А |
| Вольт-амперная характеристика | 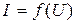
| Вебер-амперная характеристика | 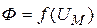
|
2.2. РАСЧЕТ МАГНИТНЫХ ЦЕПЕЙ ПРИ ПОСТОЯННЫХ ПОТОКАХ
2.2.1. ОБЩАЯ ХАРАКТЕРИСТИКА ЗАДАЧ И МЕТОДОВ РАСЧЕТА МАГНИТНЫХ ЦЕПЕЙ
Как отмечалось ранее, чтобы сконцентрировать магнитный поток, а также уменьшить величину МДС и мощность катушки при заданном значении магнитной индукции (магнитного потока Ф), электротехнические устройства выполняют на ферромагнитных сердечниках.
В зависимости от конфигурации магнитопровода различают неразветвленные и разветвленные магнитные цепи. Неразветвленная магнитная цепь представляет собой один магнитный контур, участки которого могут иметь различную геометрическую конфигурацию и поперечное сечение, т.е. различные участки цепи соединены между собой последовательно и по ним протекает один и тот же магнитный поток. Разветвленные магнитные цепи содержат два или более контуров. Конфигурация магнитной цепи определяется назначением аппаратов.
Указанная в 2.1.5 формальная аналогия между электрическими и магнитными цепями позволяет распространить все методы и приемы расчета нелинейных цепей постоянного тока на нелинейные магнитные цепи. При этом для наглядности можно составить эквивалентную электрическую схему замещенияисходной магнитной цепи, с использованием которой и выполняется расчет.
Нелинейность магнитных цепей определяется нелинейным характером зависимости 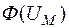 , являющейся аналогом вольт-амперной характеристики
, являющейся аналогом вольт-амперной характеристики 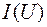 и определяемой характеристикой ферромагнитного материала
и определяемой характеристикой ферромагнитного материала 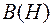 . При расчете магнитных цепей при постоянных потоках обычно используют основную кривую намагничивания (ОКН). Петлеобразный характер зависимости
. При расчете магнитных цепей при постоянных потоках обычно используют основную кривую намагничивания (ОКН). Петлеобразный характер зависимости 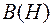 учитывается при расчете электромагнитных устройств с переменными магнитными потоками.
учитывается при расчете электромагнитных устройств с переменными магнитными потоками.
При расчете магнитных цепей на практике встречаются два типа задач:
1. Прямая задача (задача синтеза) - задача определения величины МДС (тока I и числа витков w катушки), необходимой для создания заданного магнитного потока (магнитной индукции) на каком-либо участке магнитопровода с известными геометрическими размерами и материалом;
2. Обратная задача(задача анализа) - задача нахождения потоков (магнитных индукций) на отдельных участках цепи по известным значениям МДС, геометрическим размерам и материалу магнитопровода.
Следует отметить, что задачи второго типа являются обычно более сложными и трудоемкими в решении.
Перед расчетом магнитной цепи, независимо от решаемой задачи, необходимо определить (указать на схеме) направления МДС, если известны направления токов в обмотках (по правилу правого винта), или задаться их положительными направлениями, если их нужно определить.
Затем задаются положительными направлениями магнитных потоков (в ветвях с МДС направления потоков совпадают с направлением МДС, в других ветвях они выбираются произвольно). Направления падений магнитного напряжения в ветвях совпадают с направлениями потоков в этих ветвях.
После этого переходят к составлению эквивалентной схемы замещения (если необходимо) и расчетам.
2.2.2. РАСЧЕТ НЕРАЗВЕТВЛЕННЫХ МАГНИТНЫХ ЦЕПЕЙ
Прямая задача.
В качестве исходных данных для расчета задаются:
- конфигурация и основные геометрические размеры магнитной цепи;
- кривая (кривые) намагничивания ферромагнитного материала;
- магнитный поток или магнитная индукция в каком-либо сечении магнитопровода.
Требуется найти МДС, токи обмоток или, при известных значениях последних, число витков.
Решение прямой задачи осуществляется в следующей последовательности:
1. Магнитная цепь разбивается на участки одинакового сечения 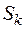 магнитопровода;
магнитопровода;
2. По заданным геометрическим размерам магнитной цепи определяется длина средней силовой линии 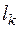 каждого участка;
каждого участка;
3. Исходя из постоянства магнитного потока Ф в любом сечении магнитопровода, по известным сечениям участков 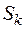 находится магнитная индукция для каждого участка:
находится магнитная индукция для каждого участка: 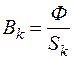 .
.
4. По основной кривой намагничивания для найденных значений индукции 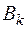 находится напряженность поля
находится напряженность поля 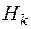 на каждом участке. В воздушном зазоре напряженность магнитного поля
на каждом участке. В воздушном зазоре напряженность магнитного поля 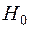 определяется по выражению:
определяется по выражению:
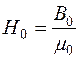 или
или 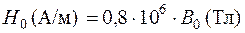 .
.
5. По найденным напряженностям магнитного поля 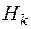 и длинам участков
и длинам участков 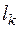 находятся падения магнитного напряжения на участках
находятся падения магнитного напряжения на участках
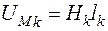 .
.
6. По второму закону Кирхгофа для магнитной цепи находится значение искомой МДС путем суммирования падений магнитного напряжения вдоль контура:
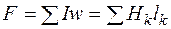 .
.
Пример 1. Рассмотрим пример расчета неразветвленной магнитной цепи с воздушным зазором (рис.2.2).
Дано: 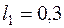 м,
м, 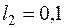 м,
м, 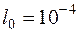 м;
м; 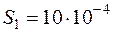 м2,
м2, 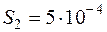 м2;
м2; 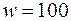 витков. Кривая намагничивания материала сердечника приведена на рис.2.3. Индукция в воздушном зазоре
витков. Кривая намагничивания материала сердечника приведена на рис.2.3. Индукция в воздушном зазоре 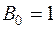 Тл.
Тл.
Определить ток I намагничивающей обмотки.

Решение
Принимаем «сечение» воздушного зазора 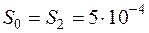 м2, т.е. пренебрегаем выпучиванием магнитного потока в зазоре.
м2, т.е. пренебрегаем выпучиванием магнитного потока в зазоре.
Так как поток в магнитопроводе один - Ф, то индукция во втором участке магнитопровода будет 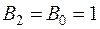 Тл.
Тл.
1. Индукция на первом участке магнитопровода
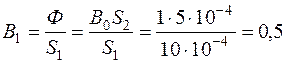 Тл.
Тл.
2. Зная индукции В1 и В2 по ОКН (см. рис.2.3) определяем напряженности поля 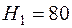 А/м,
А/м, 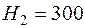 А/м.
А/м.
3. Напряженность магнитного поля в воздушном зазоре
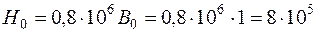 А/м.
А/м.
4. Суммарное магнитное падение напряжения найдем по второму закону Кирхгофа
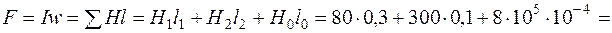
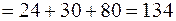 А.
А.
5. Ток в обмотке
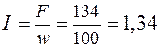 А.
А.
Основным допущением в данном расчете является то, что поток Ф в любом сечении магнитопровода полагается одинаковым. В реальных условиях небольшая часть созданного магнитного потока замыкается по воздуху. Эта часть  магнитного потока называется потоком рассеяния.
магнитного потока называется потоком рассеяния.
При увеличении воздушного зазора общее магнитное сопротивление цепи растет, растет и доля магнитного потока рассеяния, и он может оказаться соизмеримым с основным потоком. Это потребует увеличения тока I намагничивающей обмотки для обеспечения требуемого значения магнитной B индукции или магнитного потока Ф.
Обратная задача.
Решение обратной задачи осуществляется в следующей последовательности:
1. Задаются значениями потока и определяют для них МДС 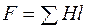 , как при решении прямой задачи. При этом следует стремиться подобрать два достаточно близких значения потока, чтобы получить
, как при решении прямой задачи. При этом следует стремиться подобрать два достаточно близких значения потока, чтобы получить  несколько меньшую и несколько большую заданной величины МДС.
несколько меньшую и несколько большую заданной величины МДС.
2. По полученным данным строится часть характеристики 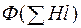 магнитной цепи (вблизи заданного значения МДС), и по ней определяется поток, соответствующий заданной величине МДС.
магнитной цепи (вблизи заданного значения МДС), и по ней определяется поток, соответствующий заданной величине МДС.
При расчете неразветвленных магнитных цепей, содержащих воздушные зазоры, удобно использовать метод пересечений, при котором искомое решение определяется точкой пересечения нелинейной вебер-амперной характеристики нелинейной части цепи и линейной характеристики линейного участка, строящейся на основании уравнения
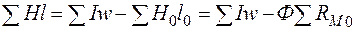 ,
,
где  - магнитное сопротивление воздушного зазора.
- магнитное сопротивление воздушного зазора.
Пример 2. Рассмотрим магнитную цепь примера 1 (см. рис.2.2).
Для тех же геометрических размеров, числа витков и ОКН материала сердечника (см. рис.2.3) требуется определить магнитный поток Ф при токе намагничивающей обмотки 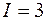 А.
А.
Решение
Расчет обратной задачи основан на построении вебер-амперных характеристик 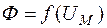 .
.
1. Для заданной магнитной цепи составим электрическую схему замещения (рис.2.4).

Магнитная цепь содержит два участка с различными сечениями. Это учитывается введением двух нелинейных магнитных сопротивлений 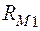 и
и 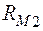 . Влияние воздушного зазора учтено линейным сопротивлением
. Влияние воздушного зазора учтено линейным сопротивлением 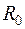 .
.
2. Составим уравнение по второму закону Кирхгофа
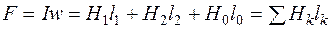 . (2.2)
. (2.2)
3. Задаваясь различными значениями магнитной индукции в воздушном зазоре 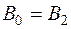 , находим индукцию
, находим индукцию
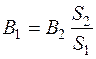 .
.
4. По ОКН материала сердечника (см. рис.2.3) по значениям индукций В1 и В2 находим напряженности поля H1 и H2 соответствующих участков.
5. Напряженность поля в воздушном зазоре находим по формуле
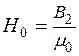 .
.
6. По выражению (2.2) находим падения магнитного напряжения вдоль цепи 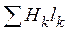 .
.
7. По магнитной индукции 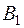 или В2 определяем магнитный поток в цепи
или В2 определяем магнитный поток в цепи
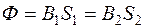 .
.
Результаты расчетов сводим в табл.2.2.
Таблица 2.2
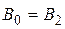 , Тл , Тл
| 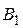 , Тл , Тл
| 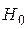 , А/м , А/м
| 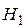 , А/м , А/м
| 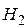 , А/м , А/м
|  , А , А
| Ф, Вб |
| 0,5 | 0,25 | 4∙105 | 9+5+40=54 | 50∙10-4 | ||
| 0,5 | 8∙105 | 15+30+80=125 | 100∙10-4 | |||
| 1,2 | 0,6 | 9,6∙105 | 30+60+96=186 | 120∙10-4 | ||
| 1,4 | 0,7 | 11,2∙105 | 45+160+112=317 | 140∙10-4 |
8. По данным из табл.2.2 строим вебер-амперную характеристику (рис.2.5).

9. По вебер-амперной характеристике при значении МДС 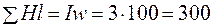 А находим искомый магнитный поток
А находим искомый магнитный поток 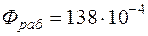 Вб (см. рис.2.5).
Вб (см. рис.2.5).
Пример 3. Определить индуктивность катушки с ферромагнитным сердечником (рис.26,а), кривая намагничивания которого изображена на рис.2.6,б, если 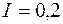 А,
А, 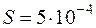 м2,
м2, 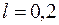 м,
м, 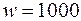 витков.
витков.

Р и с. 2.6
Решение
С помощью закона полного тока определяем напряженность магнитного поля
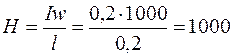 А/м.
А/м.
По кривой намагничивания при  А/м находим магнитную индукцию
А/м находим магнитную индукцию
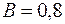 Тл.
Тл.
Магнитный поток внутри катушки
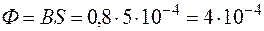 Вб.
Вб.
Индуктивность катушки
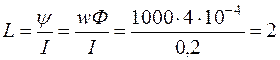 Гн.
Гн.
В соответствии с определением потокосцепления для рассматриваемой катушки с ферромагнитным сердечником имеем
 (2.3)
(2.3)
и на основании закона полного тока
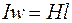 ,
,
откуда
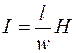 . (2.4)
. (2.4)
Из соотношений (2.3) и (2.4) следует, что функция 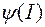 качественно имеет такой же вид, что и
качественно имеет такой же вид, что и 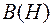 .
.
Если магнитную проводимость сердечника обозначить через 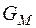 , то поток
, то поток 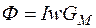 и потокосцепление
и потокосцепление 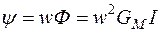 , откуда
, откуда
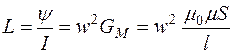 . (2.5)
. (2.5)
Используя соотношение (2.5), покажем влияние воздушного зазора на индуктивность катушки.
Пусть магнитопровод катушки на рис.2.6,а имеет воздушный зазор длиной l0. Тогда полное магнитное сопротивление контура
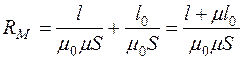 ,
,
откуда
 .
.
При 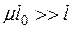 можно считать
можно считать 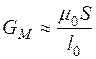 ,
,
Следовательно
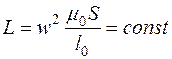 .
.
Таким образом, воздушный зазор линеаризует характеристику катушки с ферромагнитным сердечником. Зазор, для которого выполняется неравенство 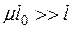 , называется большим зазором.
, называется большим зазором.
2.2.3. РАСЧЕТ РАЗВЕТВЛЕННЫХ МАГНИТНЫХ ЦЕПЕЙ
Разветвленной называется магнитная цепь, состоящая из нескольких контуров, содержащих МДС. Расчет разветвленных магнитных цепей основан на совместном применении первого и второго законов Кирхгофа для магнитных цепей, для них применимы основанные на этих законах методы расчета нелинейных электрических цепей. При этом магнитную цепь желательно изобразить эквивалентной электрической схемой замещения, пользуясь формальной аналогией магнитных и электрических цепей.
Прямая задача.
Последовательность решения задач данного типа в целом соответствует рассмотренной выше последовательности решения прямой задачи для неразветвленной цепи. При этом для определения магнитных потоков на участках магнитопровода, для которых магнитная напряженность известна или может быть вычислена на основании второго закона Кирхгофа, следует использовать алгоритм
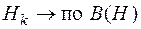 ,
, 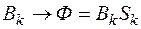 .
.
В остальных случаях неизвестные магнитные потоки определяются на основании первого закона Кирхгофа для магнитных цепей.
Пример 4. Для разветвленной магнитной цепи на рис.2.7 при заданных геометрии и характеристике B(H) ферромагнитного сердечника определить МДС F = Iw, необходимую для создания в воздушном зазоре индукции В0.

Последовательность решения задачи в общем виде следующая:
1. Задаем положительные направления магнитных потоков Ф1, Ф2, Ф3 в стержнях магнитопровода (см. рис.2.7).
2. Определяем напряженность в воздушном зазоре 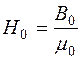 и по зависимости B(H) для B3 = B0 – значение напряженности H3.
и по зависимости B(H) для B3 = B0 – значение напряженности H3.
3. По второму закону Кирхгофа для правого контура можно записать
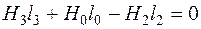 ,
,
откуда находим напряженность H2 и по зависимости B(H) – индукцию B2.
4. В соответствии с первым законом Кирхгофа
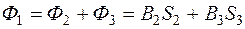 .
.
Тогда 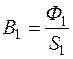 , и по зависимости B(H) определяем H1.
, и по зависимости B(H) определяем H1.
5. В соответствии со вторым законом Кирхгофа для искомой МДС имеет место уравнение
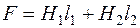 .
.
Обратная задача.
Замена магнитной цепи эквивалентной электрической схемой замещения позволяет решать задачи данного типа с использованием всех графических методов и приемов, применяемых при анализе аналогичных нелинейных электрических цепей постоянного тока.
В этом случае при расчете магнитных цепей, содержащих два узла (такую конфигурацию имеет большое число используемых на практике магнитопроводов), широко используется метод двух узлов. Идея решения данным методом заключается в следующем:
1. Вычисляются зависимости 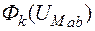 потоков во всех k ветвях магнитной цепи в функции общей величины - магнитного напряжения
потоков во всех k ветвях магнитной цепи в функции общей величины - магнитного напряжения  между узлами a и b цепи.
между узлами a и b цепи.
2. Определяется, в какой точке графически реализуется первый закон Кирхгофа 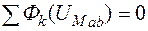 . Соответствующие данной точке потоки являются решением задачи.
. Соответствующие данной точке потоки являются решением задачи.
Пример 5.Рассчитать разветвленную магнитную цепь, представленную на рис.2.8. Геометрические размеры магнитопровода l1, l2, l3, l0, S1 = S2 = S3 = S, числа витков катушек w1 и w2, а так же токи I1 и I2 и основную кривую намагничивания 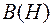 считаем заданными.
считаем заданными.
Требуется определить магнитные потоки Ф1, Ф2, Ф3 в стержнях магнитопровода.

Расчет магнитной цепи начинаем с определения направлений МДС и потоков в стержнях магнитопровода.
Направления МДС определяем по правилу правого винта или с помощью мнемонического правила: если сердечник мысленно охватить правой рукой, расположив пальцы по току в обмотке, по отогнутый большой палец укажет направление МДС.
В рассматриваемом примере МДС F1 направлена вверх, а МДС F2 – вниз. Тогда магнитный поток Ф1 направляем вверх, а поток Ф2 - вниз. Направление потока Ф3 в стержне, не содержащем МДС, выбираем прои
Дата добавления: 2017-09-01; просмотров: 4146;











