ПЕРЕХОД ОТ ИЗОБРАЖЕНИЙ К ОРИГИНАЛАМ

Переход от полученного операторного изображения искомой функции к оригиналу может быть осуществлен несколькими способами:

1. С помощью обратного преобразования Лапласа

,

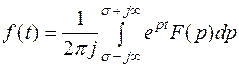На практике этот способ применяется редко.

2. По таблицам соответствия между оригиналами и изображениями.

В специальной литературе имеется достаточно большое число формул соответствия, охватывающих практически все задачи электротехники. Согласно данному способу необходимо получить операторное изображение искомой величины в виде, соответствующем табличному, после чего найти по таблице выражение оригинала.

Например, для операторного изображения тока в цепи на рис.1.22 можно записать

.

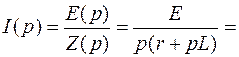
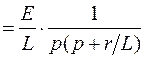Полученное изображение приведено к табличному виду и в соответствии с данными табл.1.2 получаем оригинал

,

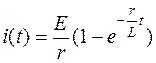что совпадает с результатом, полученным для данной цепи в 1.5.1 классическим методом расчета.

3. С помощью формулы разложения.

Пусть операторное изображение F (p) искомой функции получено в виде отношения двух полиномов по степеням p

,

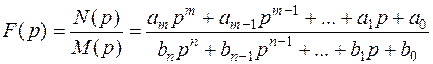причем степень числителя меньше степени знаменателя (m < n), а полином M(p) = 0 не имеет кратных корней.

Это выражение можно представить в виде суммы простых дробей [1,2]

,

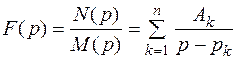где p_k - k-й корень уравнения M(p) = 0.

Для определения коэффициентов A_k умножим обе части соотношения на (p - p_k):

.

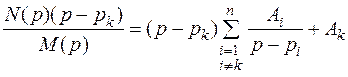При p → p_k получим

.

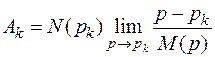Рассматривая полученную неопределенность типа по правилу Лопиталя, запишем

.

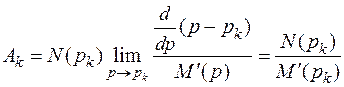Таким образом,

.

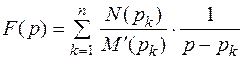Отношение 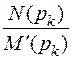есть величина постоянная, а 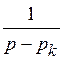является изображением функции 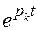(см. табл.1.2).

Учитывая свойства изображений окончательно получаем выражение для оригинала

.

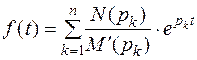Полученное выражение представляет собой формулу (теорему) разложения. Формулой разложения широко пользуются на практике и ее принято считать основной формулой для перехода от изображения к функции времени.

Примечания.

1. Если среди корней уравнения М(р) = 0 имеется нулевой корень, то соответствующее ему слагаемое в формуле разложения представляет собой составляющую искомой функции времени, обусловленную действием источника постоянного напряжения или тока.

2. Коэффициенты 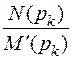в формуле разложения можно сопоставить с постоянными интегрирования A_k в классическом методе расчета.

3. Принужденной составляющей от действия источника синусоидальной ЭДС в формуле разложения соответствует слагаемое, определяемое корнем p = jω. Для сложных схем такое ее вычисление может оказаться достаточно трудоемким, поэтому принужденную составляющую в этих случаях целесообразно определять отдельно символическим методом, а свободную – операторным.

4. Для нахождения начального и конечного значений оригинала можно использовать предельные соотношения

; .

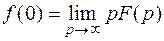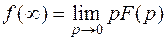Пример.

Полученное операторное изображение тока в ветви имеет вид

.

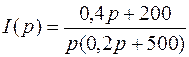Найдем оригинал этого тока .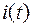

1способ.

Используем таблицу соответствия (см. табл.1.2). Для этого преобразуем изображение I(p) таким образом, чтобы получить табличное выражение.

Представим I(p) в виде суммы двух функций, которые после преобразования примут вид табличных формул:

.

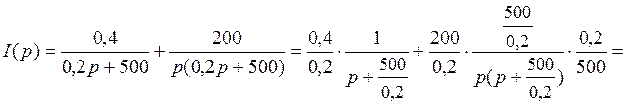
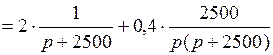В соответствии с табл.1.2 такому операторному изображению соответствует функция времени

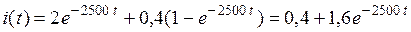А.

2способ.

Используем формулу разложения.

Для данного изображения 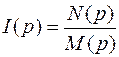имеем

; .

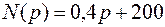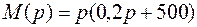Находим корни уравнения

;

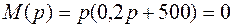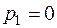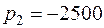; с^-1.

Находим производную

.

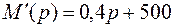Определяем необходимые значения 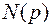и 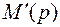при найденных корнях:

;

;

;

.

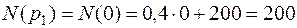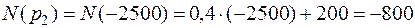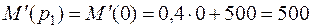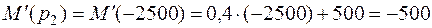Подставляя найденные значения в формулу разложения, получим функцию времени

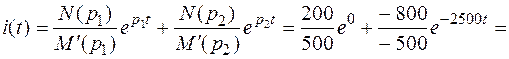
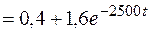А.

Отметим, что формула разложения применима при любых начальных условиях при любых практически встречающихся формах напряжения (тока) источника, воздействующего на схему. Однако, если среди корней уравнения М(р) = 0 имеются кратные корни, то рекомендуется использовать таблицы соответствия.