ПОСЛЕДОВАТЕЛЬНОСТЬ РАСЧЕТА ОПЕРАТОРНЫМ МЕТОДОМ

В общем случае расчет переходных процессов операторным методом включает следующие этапы:

1. Нахождение независимых начальных условий из расчета установившегося режима до коммутации.

2. Составление послекоммутационной операторной схемы замещения цепи (для простых цепей с нулевыми начальными условиями этот этап может быть пропущен).

3. Запись для операторной схемы замещения уравнений по законам Кирхгофа или другим методам расчета линейных цепей в операторной форме.

4. Решение полученных уравнений относительно изображений искомых величин.

5. Переход от найденных изображений к функциям времени (с помощью формулы разложения или таблиц соответствия).

1.7. ПРИМЕРЫ РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ

ОПЕРАТОРНЫМ методОМ

Пример 1.

Определить ток через катушку индуктивности в цепи на рис.1.23 операторным методом.

Решение

Имеем нулевое начальное условие

.

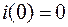Операторное сопротивление цепи

.

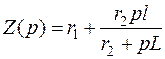Операторное изображение искомого тока

.

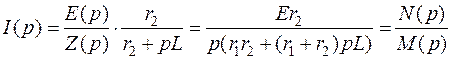Для нахождения оригинала i(t) воспользуемся формулой разложения.

Корни уравнения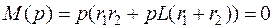

; .

;

; ;

.

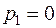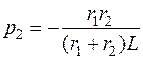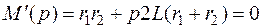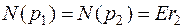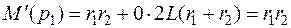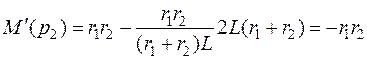Подставляя найденные значения в формулу разложения, получим

.

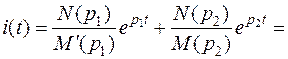
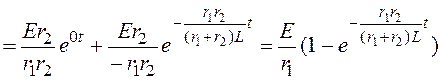Воспользуемся предельными соотношениями для проверки правильности определения начального i(0) и конечного i(∞) значений:

;

.

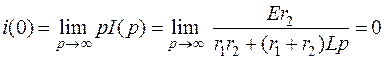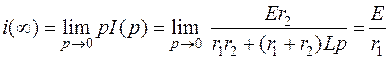Пример 2.

В цепи (рис.1.24) даны: E = 120 В, r₁ = r₂ = r₃ = 4 Ом, L = 0,1 Гн. Найти токи в ветвях после коммутации операторным методом, построить временные зависимости этих величин.

Решение

Это пример переходного процесса в цепи с ненулевым начальным условием.

Независимое начальное условие i₃(0) найдем из расчета токов в докоммутационном установившемся режиме (ключ разомкнут):

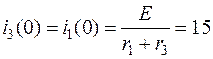А, i₂(0) = 0.

Операторная схема замещения послекоммутационной цепи приведена на рис.1.25. Ненулевое начальное условие учитывается введением в ветвь с индуктивностью внутренней ЭДС Li₃(0), направленной согласно току i₃.

Найдем изображение напряжения U_ab(p) методом двух узлов:

.

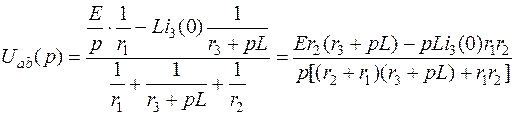После подстановки численных значений получаем

.

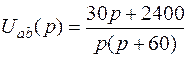Изображение тока I₂(p) найдем по закону Ома в операторной форме

.

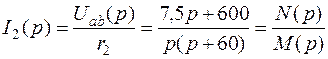Переход от полученного изображения 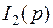к оригиналу 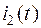выполним с помощью формулы разложения.

Корни уравнения :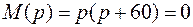

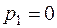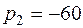; с^-1.

Производная .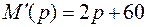

Численные значения

; ; ; .

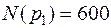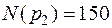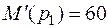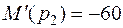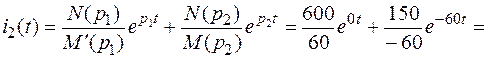
Подставляя найденные значения в формулу разложения, получаем оригинал ток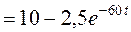а

А.

Изображение тока I₁(p) найдем с помощью второго закона Кирхгофа или закона Ома для участка цепи с ЭДС в операторной форме

.

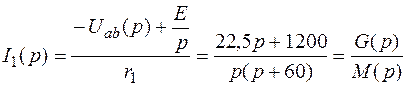Переход от полученного изображения 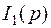к оригиналу 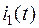выполним с помощью формулы разложения.

Численные значения

; ; ; .

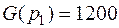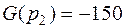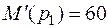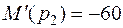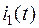
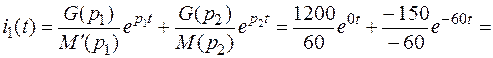
Подставляя найденные значения в формулу разложения, получаем оригинал ток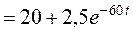а

А.

Зная ток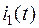и и 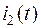, найдем ток 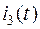по первому закону Кирхгоф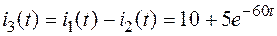а

А.

Кривые токов в ветвях представлены на рис.1.26.

Отметим, что в момент коммутации в ветвях с r₁ и r₂ имеют место скачки токов, что не противоречит законам коммутации, так как в этих ветвях отсутствуют накопители энергии. В ветви с индуктивностью скачка тока не происходит, что соответствует требованию первого закона коммутации.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Чем обусловлены переходные процессы в электрических цепях?

2. Что называется коммутацией?

3. Что понимают под начальными условиями переходного процесса? Какие из начальных условий относятся к независимым?

4. Сформулируйте законы коммутации.

5. В каких случаях необходимо использовать законы коммутации в обобщенной форме?

6. Как определяется порядок дифференциального уравнения, описывающего переходный процесс?

7. Для каких цепей применим классический метод расчета переходных процессов?

8. В чем состоит сущность классического метода расчета переходных процессов?

9. Как рассчитывается принужденная составляющая тока (напряжения) в классическом методе? Чем определяется ее вид?

10. Как рассчитывается свободная составляющая тока (напряжения) в классическом методе? Чем определяется ее вид?

11. В каких цепях и при каких условиях возможен колебательный характер переходного процесса?

12. Может ли в одной части линейной цепи протекать колебательный переходный процесс, а в другой – апериодический?

13. Может ли протекать колебательный переходный процесс в цепях первого порядка (с одним накопителем энергии)? Почему?

14. Почему можно разрывать ветвь с конденсатором и нельзя – ветвь с индуктивным элементом?

15. Чем определяется число корней характеристического уравнения?

16. Почему корни характеристического уравнения не зависят от того, относительно какой переменной было записано дифференциальное уравнение?

17. Что такое постоянная времени цепи?

18. Как можно определить постоянную времени в цепи с одним накопителем энергии по осциллограмме тока или напряжения в какой-либо ветви?

19. Влияет ли на постоянную времени цепи тип питающего устройства: источник напряжения или источник тока?

20. Как влияет на характер переходного процесса в r-L-C-контуре величина сопротивления r и почему?

21. В чем заключается сущность расчета переходных процессов операторным методом?

22. Какие этапы включает в себя операторный метод расчета переходных процессов?

23. Как записывается операторное сопротивление участка цепи?

24. Что такое операторная схема замещения?

25. Как при расчете операторным методом учитываются ненулевые независимые начальные условия?

26. Что такое внутренняя ЭДС? Когда необходимо ее учитывать?

27. Какими способами осуществляется переход от изображения к оригиналу?

28. Для чего используются предельные соотношения?

29. Как связаны изображение и оригинал в формуле разложения?

30. Как целесообразно проводить расчет переходных процессов в сложных цепях при синусоидальном источнике питании?

31. Проведите сравнительный анализ классического и операторного методов.

2. МАГНИТНЫЕ ЦЕПИ

2.1. НЕЛИНЕЙНЫЕ МАГНИТНЫЕ ЦЕПИ ПРИ

ПОСТОЯННЫХ ПОТОКАХ