ПЕРЕХОДНЫЕ ПРОЦЕССЫ ПРИ ПОДКЛЮЧЕНИИ
ЦЕПИ r – L – C К ИСТОЧНИКУ ЭДС
Дифференциальное уравнение, описывающее процессы в цепи на рис.1.14 после коммутации относительно 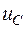 *, получено в 1.4.1:
*, получено в 1.4.1:
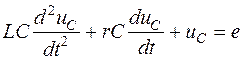 .
.
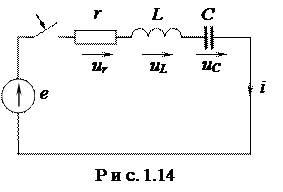 Рассмотрим два случая:
Рассмотрим два случая:
а) Источник постоянной ЭДС
e(t) = E;
б) Источник синусоидальной ЭДС
e(t) = Emsin(ωt + ψ).
Независимые начальные условия 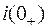 и
и 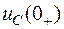 получаем с помощью первого закона коммутации из анализа докоммутационного режима (ключ разомкнут, цепь отключена от источника энергии, конденсатор в общем случае предварительно заряжен до напряжения
получаем с помощью первого закона коммутации из анализа докоммутационного режима (ключ разомкнут, цепь отключена от источника энергии, конденсатор в общем случае предварительно заряжен до напряжения 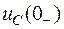 ). Следовательно, имеем:
). Следовательно, имеем:
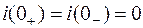 ;
;
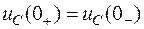 .
.
Согласно методике расчета переходных процессов классическим методом для напряжения на конденсаторе можно записать
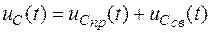 .
.
Для случая а) в установившемся режиме после коммутации имеем цепь постоянного тока (сопротивление индуктивности L равно нулю, а емкости С - бесконечности) с разрывом на месте емкости. Ток в этом режиме равен нулю, а напряжение источника приложено к емкости С.
Тогда для случая а) принужденная составляющая напряжения
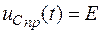 .
.
Характеристическое уравнение цепи (см. 1.4.2)
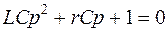 ,
,
решая которое, получаем
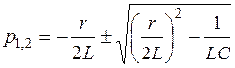 .
.
В зависимости от соотношения параметров цепи r, L и C возможны три типа корней характеристического уравнения и соответственно три варианта выражения для свободной составляющей:
1. Корни вещественны и отличны друг от друга 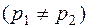 , что имеет место при условии
, что имеет место при условии 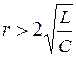 .
.
В этом случае свободная составляющая напряжения на конденсаторе в общем виде (см. табл.1.1)
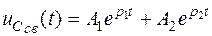
(апериодический характер свободного режима).
2. Корни вещественны и равны друг другу, что имеет место при условии 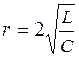 . При этом корни
. При этом корни 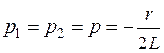 . Характер процесса в этом случае не отличается от рассмотренного выше случая, т.е. также является апериодическим. При уменьшении r ниже значения
. Характер процесса в этом случае не отличается от рассмотренного выше случая, т.е. также является апериодическим. При уменьшении r ниже значения 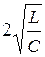 разряд становится колебательным. Поэтому данный случай разряда конденсатора называют предельным (критическим) апериодическим, а величину rкр
разряд становится колебательным. Поэтому данный случай разряда конденсатора называют предельным (критическим) апериодическим, а величину rкр 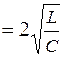 – критическим сопротивлением.
– критическим сопротивлением.
В этом случае свободная составляющая напряжения на конденсаторе в общем виде (см. табл.1.1)
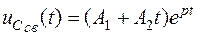
(предельный апериодический характер свободного режима).
3. Корни комплексно-сопряженные, что имеет место при условии 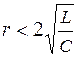 . При этом
. При этом 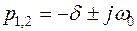 , где
, где 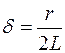 - коэффициент затухания;
- коэффициент затухания; 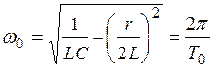 - угловая частота собственных колебаний; T0 – период собственных колебаний.
- угловая частота собственных колебаний; T0 – период собственных колебаний.
В этом случае свободная составляющая напряжения на конденсаторе в общем виде (см. табл.1.1)
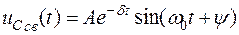
(колебательный характер свободного режима).
В каждом из рассмотренных случаев для нахождения свободной составляющей необходимо определить две постоянных интегрирования (А1, А2или А, ψ). Следовательно, необходимо получить еще одно уравнение, связывающее искомые величины. Для этого продифференцируем уравнения для свободных составляющих по времени (см. 1.4.3).
Для апериодического характера переходного процесса можно записать
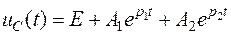 .
.
Для нахождения постоянных интегрирования A1 и A2, учитывая, что в общем случае 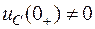 и по первому закону коммутации
и по первому закону коммутации 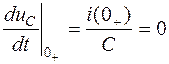 , запишем для момента времени
, запишем для момента времени 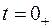 два уравнения:
два уравнения:
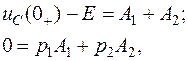
решив которые, получим A1 и A2:
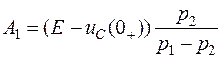 ;
; 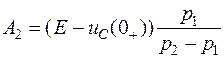 .
.
Таким образом, напряжение на конденсаторе в переходном процессе
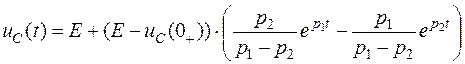 .
.
Ток апериодического переходного процесса
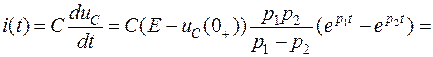
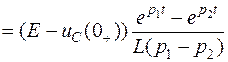 .
.
Напряжение на катушке индуктивности
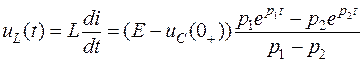 .
.
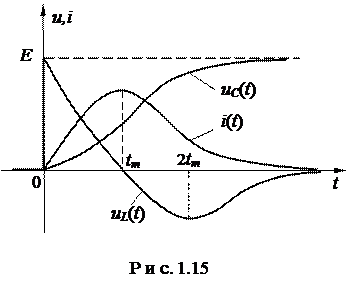
На рис.1.15 представлен качественный вид кривых 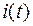 ,
, 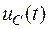 и
и 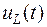 , соответствующих апериодическому характеру переходного процесса при нулевых начальных условиях (
, соответствующих апериодическому характеру переходного процесса при нулевых начальных условиях ( 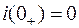 ;
; 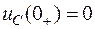 ).
).
Момент времени 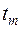 , соответствующий максимуму тока в цепи, находится из условия
, соответствующий максимуму тока в цепи, находится из условия 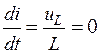 и равен
и равен 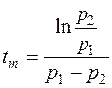 .
.
Для предельного апериодического характера переходного процесса можно записать
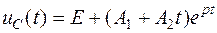 .
.
Для начального момента времени t = 0+ имеем:
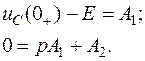
Откуда получим A1 и A2
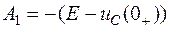 ;
; 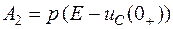 .
.
Таким образом, напряжение на конденсаторе в переходном процессе
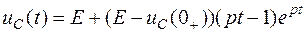 .
.
Ток предельного апериодического переходного процесса
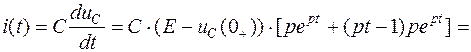
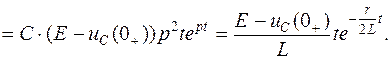
Для колебательного характера переходного процесса можно записать
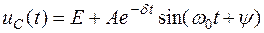 .
.
Для нахождения постоянных интегрирования A и ψ запишем для момента времени t = 0+
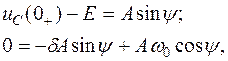
откуда
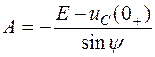 и
и 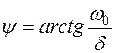 .
.
Учтем также, что
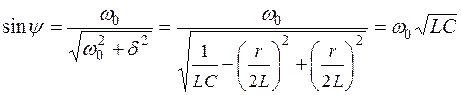 .
.
Тогда напряжение на конденсаторе в переходном процессе
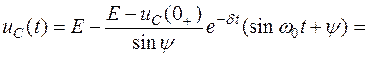 .
.
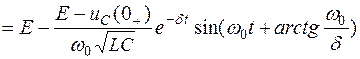 .
.
Ток колебательного переходного процесса
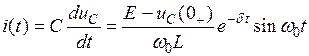 .
.

На рис.1.16 представлен качественный вид кривых 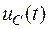 и
и 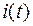 , соответствующих колебательному переходному процессу при нулевых начальных условиях (
, соответствующих колебательному переходному процессу при нулевых начальных условиях ( 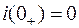 ;
; 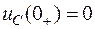 ).
).
В случае б) при подключении r-L-C-цепи к источнику синусоидальной ЭДС для нахождения принужденных составляющих тока в цепи и напряжения на конденсаторе следует воспользоваться символическим методом расчета, в соответствии с которым
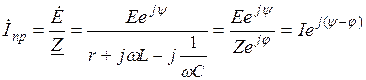
и
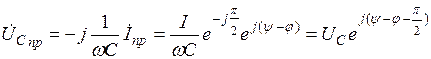 ,
,
где 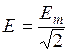 ;
; 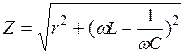 ;
; 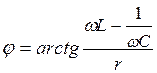 .
.
Таким образом, учитывая, что амплитудные значения синусоидальных величин 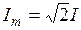 и
и 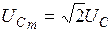 , получаем выражения принужденных составляющих тока
, получаем выражения принужденных составляющих тока 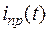 и напряжения на конденсаторе
и напряжения на конденсаторе 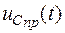
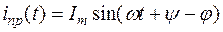 ;
;
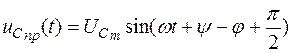 .
.
Для свободного режима в случае синусоидального источника ЭДС также существуют три варианта в зависимости от вида корней характеристического уравнения:
1. r > Rкр; p1 ≠ p2 (апериодический характер);
2. r = Rкр; p1 = p2 (предельный апериодический характер);
3. r < Rкр; p1,2 = – δ ± jω0 (колебательный характер).
Наибольший интерес представляет третий режим, связанный с появлением во время переходного процесса собственных колебаний с частотой ω0. При этом возможны, в зависимости от соотношения частот собственных колебаний и напряжения источника, три характерные варианта: а) ω >> ω0; б) ω << ω0; в) ω = ω0, которые представлены на рис.1.17.
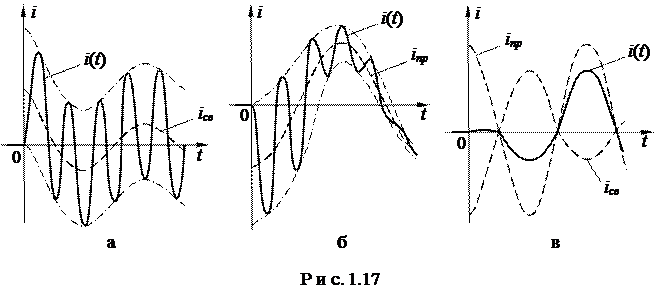
Если значение угловой частоты ω0 свободных колебаний почти равно угловой частоте ω источника питания(ω0 ≈ ω), то сложение принужденной и свободной составляющих дает колебание, для которого характерно биение амплитуды [1,2].
1.6. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
ОСНОВНЫЕ ПОЛОЖЕНИЯ
Сущность операторного метода заключается в том, что функции времени f (t), которую называют оригиналом, ставится в соответствие функция F (p), которую называют изображением.Новая переменная p = s + jω является комплексной переменной.
В результате этого производные и интегралы от оригиналов заменяются алгебраическими функциями от соответствующих изображений (дифференцирование заменяется умножением на оператор р, а интегрирование – делением на него [1,2]), что в свою очередь определяет переход от системы интегро-дифференциальных уравнений к системе алгебраических уравнений относительно изображений искомых функций. При решении этих уравнений находятся изображения и далее путем обратного перехода – оригиналы. Важнейшим моментом при этом в практическом плане является необходимость определения только независимых начальных условий uC (0) и iL(0), что существенно облегчает расчет переходных процессов в цепях высокого порядка по сравнению с классическим методом на этапе определения постоянных интегрирования.
Изображение F (p) заданной функции f (t) определяется в соответствии с прямым преобразованием Лапласа:
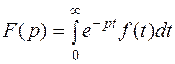 .
.
 Сокращенно соответствие между изображением и оригиналом обозначается как:
Сокращенно соответствие между изображением и оригиналом обозначается как:
F (p) f (t).
Следует отметить, что если оригинал f (t) увеличивается с ростом t, то для сходимости интеграла необходимо более быстрое убывание модуля 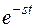 . Функции, встречающиеся на практике при расчете переходных процессов в электрических цепях, этому условию удовлетворяют.
. Функции, встречающиеся на практике при расчете переходных процессов в электрических цепях, этому условию удовлетворяют.
В качестве примера в табл.1.2 приведены операторные соотношения для наиболее характерных функций, встречающихся при анализе переходных режимов в электрических цепях.
Таблица 1.2
| f(t) | А=const | t | 
| 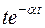
| 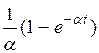
| sinωt | cosωt |
| F(p) | 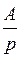
| 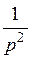
| 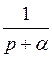
| 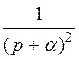
| 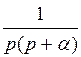
| 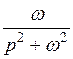
| 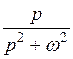
|
Отметим некоторые свойства изображений, полученных прямым преобразованием Лапласа:
1. Изображение суммы функций равно сумме изображений слагаемых:
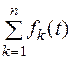
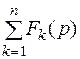
1.  При умножении оригинала на коэффициент на тот же коэффициент умножается изображение:
При умножении оригинала на коэффициент на тот же коэффициент умножается изображение:
A f (t) AF (p).
С использованием этих свойств и данных табл.1.2, можно показать, например, что
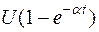
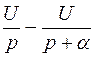 .
.
Найдем изображения напряжения на катушке индуктивности и конденсаторе.
Из курса математики известно изображение производной от функции f (t)
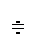
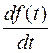
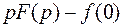 ,
,
где f (0) – начальное значение функции f (t).
Таким образом, для напряжения на индуктивном элементе можно записать:
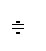
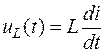
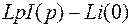 .
.
Отсюда получаем операторное сопротивление катушки индуктивности
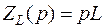 .
.
Известно также изображение интеграла от функции f (t)
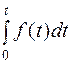
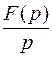 .
.
Для напряжения на конденсаторе в общем случае можно записать:
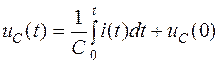 .
.
Тогда его операторное изображение
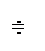
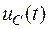
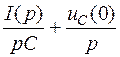
Отсюда получаем операторное сопротивление конденсатора
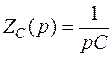 .
.
Дата добавления: 2017-09-01; просмотров: 2109;











