ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ
Если две плоскости не параллельны, то они обязательно пересекаются и результатом их пересечения является прямая.
Рассмотрим сначала частные случаи пересечение двух плоскостей.
Пример 1. Пересекаются плоскость общего положения 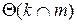 и горизонтально-проецирующая плоскость
и горизонтально-проецирующая плоскость  , заданная следом (рис.4.1).
, заданная следом (рис.4.1).
Этот случай является основой для решения задач на пересечение плоскостей в общем виде.
Так как одна из заданных плоскостей проецирующая, то все геометрические элементы, включая и линию пересечения плоскостей l, спроецируются на след этой плоскости.
На КЧ горизонтальная проекция линии пересечения определяется исходя из принадлежности ее проецирующей плоскости 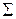 ,а фронтальная проекция – по принадлежности второй заданной плоскости.
,а фронтальная проекция – по принадлежности второй заданной плоскости.
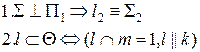
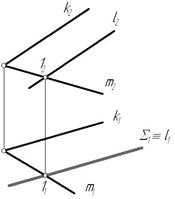
Рисунок 4.1. Решение задачи
Пример 2. Пересекаются плоскости общего положения, заданные следами (рис.4.2).

Рисунок 4.2. Решение задачи
В этом случае следы плоскости пересекаются в пределах чертежа, следовательно, линия пересечения этих плоскостей строится по двум точкам, являющимся следами линии пересечения, которые находятся в точках пересечения одноименных следов плоскостей.
Для построения линии пересечения плоскостей в общем случае необходимо найти две точки, одновременно принадлежащие этим плоскостям, или одну общую точку, если известно направление линии пересечения.
Направление линии пересечения известно в том случае, если:
1) пересекающиеся плоскости содержат взаимно-параллельные прямые (линия пересечения плоскостей параллельна этим прямым);
2) две пересекающиеся плоскости перпендикулярны третьей плоскости (линия пересечения перпендикулярна этой плоскости).
Общая точка для двух пересекающихся плоскостей в общем случае определяется с помощью вспомогательной плоскости частного положения, также пересекающей заданные плоскости по прямой (рис. 4.3).
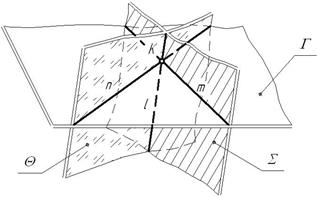
Рисунок 4.3. Модель пересечения
Общий случай: Пересекаются плоскости общего положения (рис.4.4).
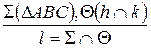 .
.

Рисунок 4.4. Решение задачи общего случая
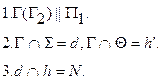
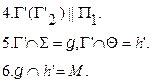
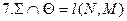 .
.
Дата добавления: 2021-09-07; просмотров: 536;











