Взаимное расположение двух плоскостей

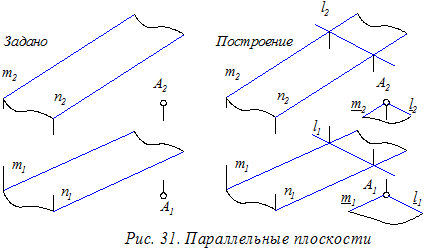Параллельные плоскости. Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Пример(рис. 31). Дано: плоскость a (m || n); точка АÏ a ; Построить плоскость b ||a; b 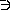А.

Построение: 1. В плоскости a проведем произвольную линию l, пресекающую прямые m и n.

2. Через точку А проведём две пересекающиеся прямые
l и m, соответственно параллельные линиям l и m. Построенные линии определят на чертеже искомую плоскость b.

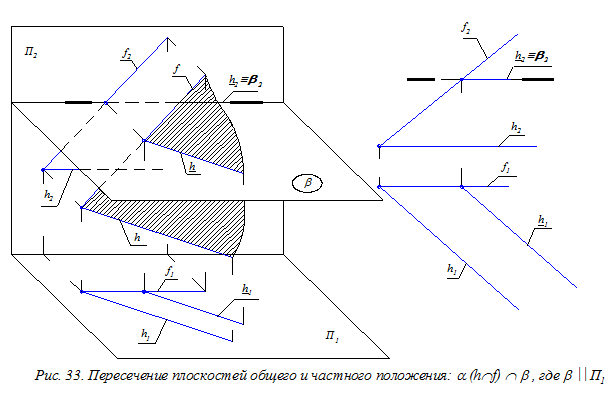Пересекающиеся плоскости. Для такого расположения двух плоскостей обычно решается следующая позиционная задача: даны две плоскости a и b. Требуется построить их линию пересечения. Сначала рассмотрим частные случаи этой задачи, когда одна из плоскостей является проецирующей плоскостью (рис. 32) или плоскостью уровня (рис. 33). В обоих случаях наличие на чертеже вырожденной проекции плоскости b частного положения определяет одну из проекций линии пересечения плоскостей (собирательное свойство вырожденной проекции плоскости). Далее строится недостающая проекция этой линии.

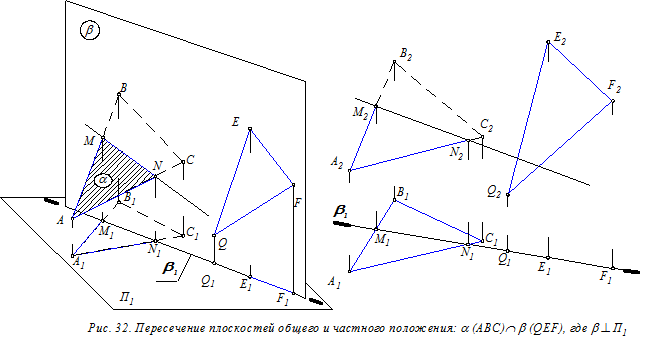Например, на рис. 32 линия пересечения обозначена MN и её горизонтальная проекция M₁N₁ определяетсягоризонтальной вырожденной проекцией b₁ плоскости b.
Если одна из заданных плоскостей является плоскостью уровня (например, на рис. 33 плоскость b ççП₁), то пересечение её с плоскостью a общего положения произойдет по горизонтали h плоскости a. Поэтому на эпюре должны быть выполнены следующие условия: h₂ º b₂ (собирательное свойство вырожденной проекции b₂) и h₁ çç h₁ (все горизонтали плоскости параллельны).

Собирательное свойство проецирующей плоскости используются в алгоритме построения линии пересечения двух плоскостей общего положения a и b (рис. 34):

1. Строим произвольную плоскость – посредник g.

2. Строим линию a пересечения плоскостей a и g.

3. Строим линию b пересечения плоскостей b и g.

4. Находим точку М пересечения линий а и b. Эта точка принадлежит искомой линии пересечения плоскостей a и b.

5. Строим новую плоскость – посредник d и повторяем пункты 2-4 алгоритма для нахождения второй точки N.

6. Проводим линию MN.

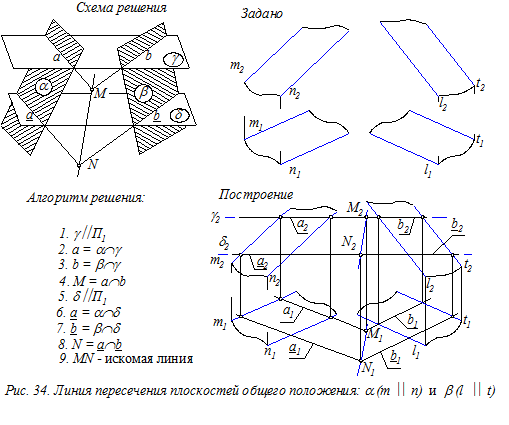На рис. 34 показана схема, алгоритм и пример решения такой задачи. При этом использованы две горизонтальные плоскости - посредники g и d, которые пересекают плоскость a по горизонталям a и a, а плоскость b - по горизонталям b и b. Заметим, что в качестве вспомогательных плоскостей можно использовать любую проецирующую плоскость.

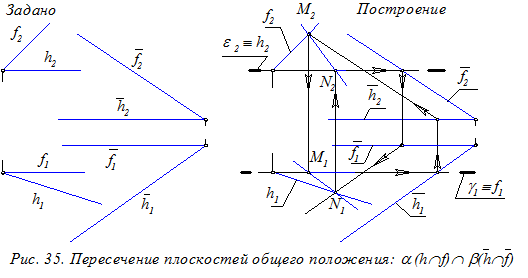
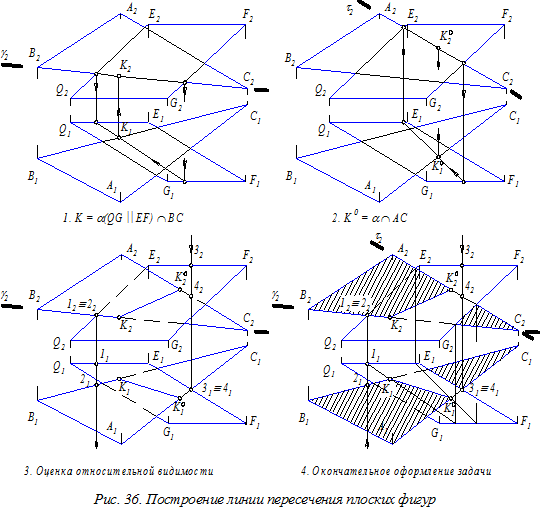
Рекомендуется проводить вспомогательные плоскости параллельно линиям, задающим плоскость, или проходящими через указанные прямые (рис. 35 и 36).

5.5. Взаимное расположение прямой линии и плоскости

Прямая линия может располагаться на плоскости, быть параллельной ей или пересекаться с этой плоскостью. Построение прямой линии, лежащей в плоскости, рассмотрено ранее, в подразделе 5.2.

Прямая линия, параллельная плоскости. Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости.

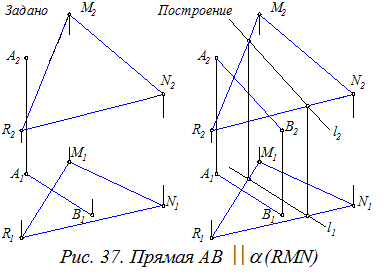
Пример. Построитьнедостающую проекцию A₂B₂ прямой АВ(A₁B₁), параллельной плоскости a(RMN).

Построение:

1. l || АВ (l₁ || A₁B₁); l Ì a.

2. A₂B₂ úú l₂.

Прямая линия, пересекающая плоскость. В этом случае прямая и плоскость будет иметь одну общую точку, нахождение которой на чертеже является одной из позиционных задач НГ.

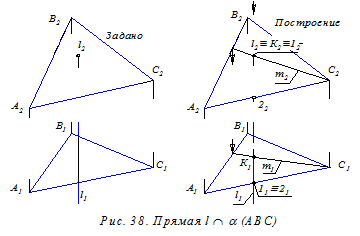
Сначала рассмотрим два частных случая (рис. 38 и 39), когда одна из фигур (прямая или плоскость) является проецирующей.

На рис. 38 показана фронтально проецирующая прямая l и плоскость a (АВС) общего положения. Вырожденная проекция l₂ прямой l обладает собирательным свойством, следовательно, фронтальная проекция К₂ точки К пересечения прямой l с плоскостью a совпадает с вырожденной проекцией прямой (К₂ºl₂). Проведя в плоскости a через точку К произвольную прямую m, находим проекцию К₁. Далее конкурирующими точками 1 и 2 оцениваем видимость прямой l относительно плоскости a.

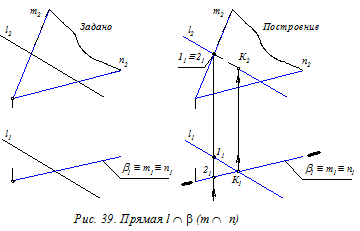
На рис. 39 показана горизонтально проецирующая плоскость b (mÇn) и прямая l общего положения. Горизонтальная вырожденная проекция b₁ плоскости b обладает собирательным свойством, следовательно, К₁ = b₁Ç l₁. По линии связи находим проекцию К₂.

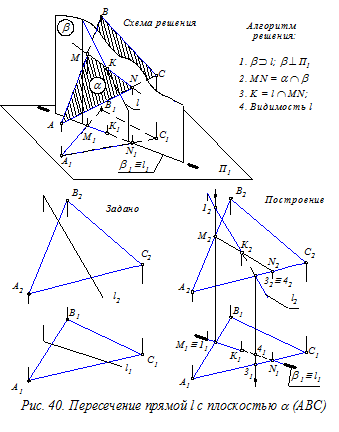
На рис. 40 показан общий случай пересечения прямой и плоскости. Для нахождения точки пересечения К используем вспомогательную горизонтально проецирующую плоскость b, проходящая через прямую l. Строим прямую MN – линию пересечения плоскостей a и b. Далее определяем точку К – пересечение линий l и MN. Конкурирующими точками оцениваем видимость прямой l относительно плоскости a.

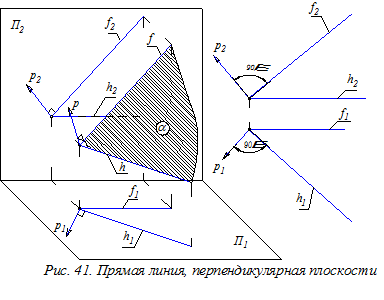Прямая линия, перпендикулярная плоскости(рис. 41).Прямая перпендикулярна плоскости {р ^ a (h Ç f)}, если её горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали этой плоскости (р₁ ^ h₁), а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали плоскости (p₂ ^ f₂).

Пример. Определить расстояние от точки А до плоскости a (QEÇEF).

Алгоритм решения (рис. 42):

1. Строим горизонталь h плоскости
(h₂ úú 0x).

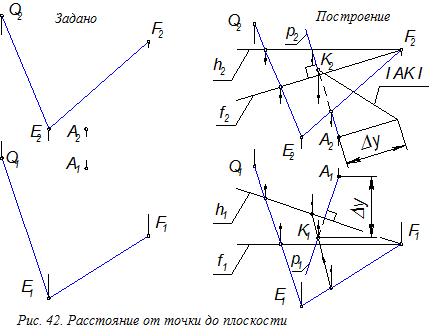2. Строим фронталь f плоскости
(f₁ úú 0x).

3. Через точку А, перпендикулярно плоскости a проводим прямую р: р₁ ^ h₁; p₂ ^ f₂.

4. Строим точку К пересечения прямой р с плоскостью a.

5. Определяем НВ отрезка АК и оцениваем видимость линии р относительно плоскости a.

Взаимно перпендикулярные плоскости. Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой плоскости.

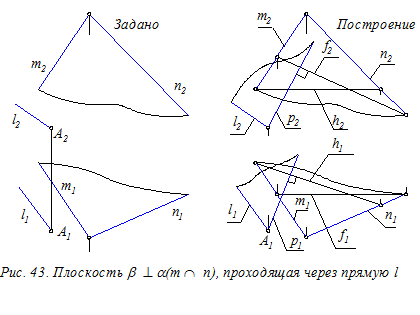
Пример. Через прямую l провести плоскость b ^ a (m Ç n).

Построение. Плоскость b может быть задана двумя пересекающими прямыми: l Ç p, где линия l задана, а линия р ^a. Для построения линии р необходимо предварительно построить горизонталь h и фронталь f плоскости a.

6. Преобразование ортогонального чертежа