Взаимное пересечение поверхностей

Решая задачу на построение линии пересечения поверхностей, необходимо установить, какое положение относительно плоскостей проекций занимает каждая поверхность и к какой задаче сводится данная задача.

1. Обе поверхности проецирующие.

Из всех рассмотренных ранее поверхностей, только цилиндр вращения и прямая призма могут быть проецирующими, так как все образующие цилиндра (и призмы) параллельны между собой и могут занимать проецирующее положение по отношению к плоскостям проекций.

На рис. 40 показано построение трех проекций линии пересечения цилиндра вращения и 4-х гранной призмы.

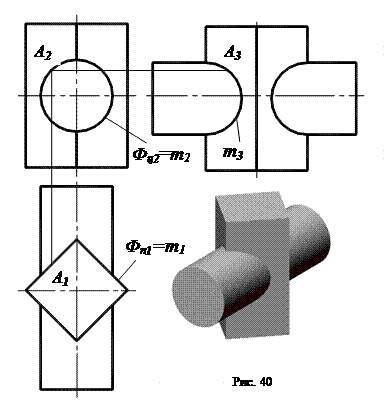Анализируя заданные геометрические Фигуры, устанавливаем, что поверхность цилиндра - фронтально - проецирующая. то есть фронтальный очерк Фц₂ цилиндра - окружность. она обладает собирательным свойством: все точки и линии, расположенные на поверхности цилиндра, проецируются на эту окружность. Поверхность 4-х гранной призмы -- горизонтально - проецирующая, то есть горизонтальная проекция призмы - прямоугольник, который обладает собирательным свойством. Таким образом, устанавливаем, что линия пересечения цилиндра и призмы на фронтальной и горизонтальной проекциях находится без дополнительных построений: горизонтальная проекция m₁= А₁В₁С₁ линии совпадает с частью очерка Фп₁ призмы в пределах очерка цилиндра; фронтальная проекция m₂= А₂В₂С₂ линии совпадает с фронтальным очерком Фц₂ цилиндра. Профильная проекция m₃= А₃В₃С₃ линии пересечения строится из условия принадлежности точек зтой линии заданным поверхностям.

2. Одна поверхность проецирующая , вторая - общего положения

На рис. 41 показано построение линии пересечения поверхностей цилиндра и конуса.

Рис. 41

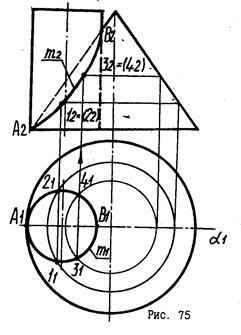
Анализируя условие задачи, устанавливаем: конус - поверхность общего вида; поверхность цилиндра - горизонтально-проецирующая, поэтому горизонтальная проекция цилиндра - окружность, обладающая собирательным свойством: на эту окружность проецируются все точки и линии. принадлежащие поверхности цилиндра, в том числе и линия пересечения.

Таким образом, горизонтальная проекция m₁ линии пересечения известна, она совпадает с окружностью - горизонтальной проекцией цилиндра.

Фронтальная проекция m₂, строится по точкам из условия принадлежности линии пересечения к поверхности конуса (с помощью вспомогательных окружностей конуса). Высшая точка В и низшая А лежат в плоскости общей симметрии a½½П ₁. Эти же точки будут являться точками видимости линии пересечения на фронтальной плоскости.

ЧАСТНЫЕ СЛУЧАИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ

(пересечение соосных поверхностей вращения, теорема Монжа)

Пересечение соосных поверхностей вращения

Соосными называются поверхности вращения, имеющие общую ось.

Свойство соосных поверхностей вращения: две любые соосные поверхности вращенияпересекаются по окружностям, проходящим через точки пересечения меридианов поверхностей.

Окружность

Рис. 42

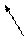
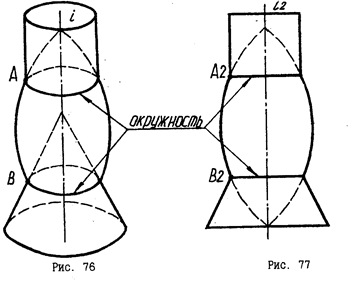
На рис. 42 видно, что общие точки А и В меридианов соосных поверхностей цилиндра и тора, тора и конуса при вращении вокруг оси i описывают окружности, общие для данных поверхностей. Эти окружности представляют собой линии пересечения этих поверхностей.

В том случае, если одна из поверхностей вращения - сфера, то рассмотренное свойство формулируется так: если центр сферы находится на оси какой-нибудь поверхности вращения, то сфера соосна этой поверхности и пересекает ее по окружностям. число которых равно числу точек пересечения (касания) главных меридианов этих поверхностей.

На рис. 43 изображены соосные поверхности - сфера и конус, главные меридианы которых пересекаются в двух точках А и В. Линиями пересечения этих поверхностей будут две окружности, проходящие через точки А и В.

На рис. 44 изображены две соосные сферы, пересекающиеся по окружности, проходящей через точку С, и соосные сфера и цилиндр, линией касания которых будет окружность, проходящая через точку D.

ТЕОРЕМА МОНЖА

Если две поверхности второго порядка описаны около третьей или вписаны в нее, то линия их пересечения распадается на две плоские кривые второго порядка. Плоскости этих кривых проходят через прямую, соединяющую точки пересечения линий касания.

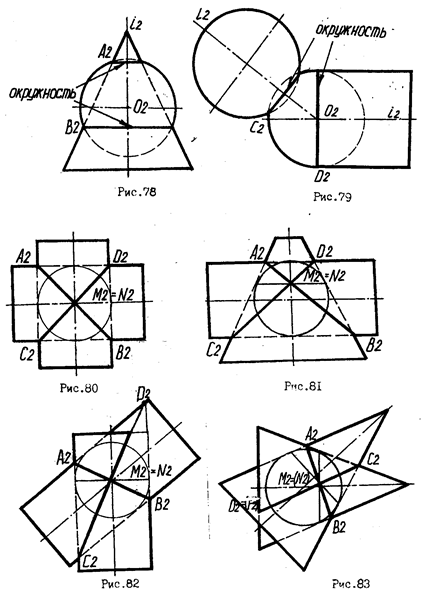
Практическое использование теоремы возможно в том случае, когда две поверхности вращения второго порядка могут быть описаны около сферы или вписаны в нее (рис.43-45).

На рис.44 показано построение фронтальных проекций линий пересечения поверхностей второго порядка, описанных около сферы. Линии пересечения представляют собой эллипсы, проходящие через опорные точки А и В, С и D. Плоскости этих эллипсов пересекаются по прямой, соединяющей М и N - точки касания поверхностей. Фронтальные проекции линий пересечения двух цилиндров по эллипсам проходят через точки А и В, С и D. Для построения точки D продолжены очерковые образующие цилиндров до их взаимного пересечения.

Теорема Монжа широко применяется при построении линий пересечения различных конструкций, выполняемых из листового материала.

Рис.45

Рис.44

Рис.43