Перпендикулярность прямой и плоскости

Из курса элементарной геометрии известно, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. Но, исходя из теоремы о проецировании прямого угла, перпендикуляр, проведенный к прямым общего положения, на КЧ проецируется с искажением. Поэтому применительно к начертательной геометрии признак перпендикулярности прямой и плоскости формулируется следующим образом.

Признак перпендикулярности прямой и плоскости:

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся линиям уровня этой плоскости.

Это связано с тем, что только к линиям уровня на плоскостях проекций можно построить прямой угол без искажения. В качестве линий уровня плоскости, при решении задач на перпендикулярность геометрических объектов, обычно выбирают горизонталь и фронталь.

Возьмем плоскость общего положения 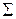и проведем в ней горизонталь и фронталь. Затем из точки пересечения линий уровня плоскости восстановим перпендикуляр АК.

На основании теоремы о проецировании прямого угла горизонтальная проекция перпендикуляра к плоскости общего положения на КЧ располагается перпендикулярно горизонтальной проекции горизонтали плоскости, а следовательно, и к ее горизонтальному следу, а фронтальная проекция перпендикуляра – фронтальной проекции фронтали и фронтальному следу.

Пример: Из точки А провести перпендикуляр к плоскости 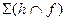и найти его основание (рис.7.3).

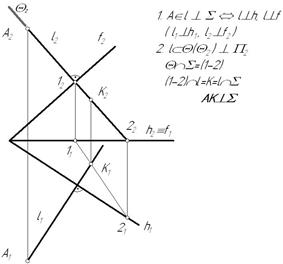
Рисунок 7.3. Решение задачи

Частный случай: Прямая перпендикулярна проецирующей плоскости (рис.7.4).

В этом случае перпендикулярная прямая будет являться линией уровня и на КЧ перпендикулярными будут вырожденная проекция плоскости (след проекций) и соответствующая проекция прямой.

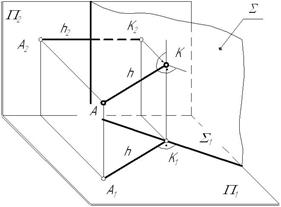
Рисунок 7.4. Модель частного случая

Пример: Найти расстояние от точки А до фронтально-проецирующей плоскости 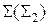(рис.7.5).

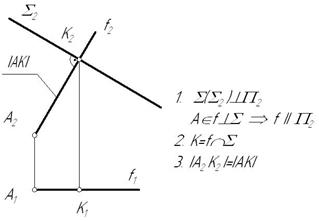
Рисунок 7.5. Решение задачи