Индексы узлов, узловых прямых и узловых плоскостей.
Если положение данного узла задано вектором  , то числа m, n и p по существу являются координатами узла решетки и называются индексами узла.
, то числа m, n и p по существу являются координатами узла решетки и называются индексами узла.
В пространственной решетке можно провести бесконечное число узловых прямых. Узловые прямые, параллельные между собой, образуют семейство узловых прямых. Для характеристики направления прямых данного семейства достаточно определить направление одной из его прямых – той, которая проходит через начало координат. Положение её по отношению к основным кристаллографическим осям однозначно характеризуется координатами ближайшего к началу координат узла. Таким образом, координаты этого узла являются индексами узловой прямой. Индексы узловых прямых при написании отличают от индексов узлов тем, что первые условились заключать в квадратные скобки (например, [u, v, w], а вторые - в двойные квадратные скобки - [ [ u, v, w ] ]).
Пространственная решетка кристалла характеризуется также различными совокупностями параллельных и равноотстоящих друг от друга узловых плоскостей, которые называются семействами узловых
(атомных) плоскостей. 
|
|






|

































Рис. 2. Семейства плоскостей. Межплоскостные расстояния.
Кратчайшее расстояние между соседними плоскостями данного семейства называется межплоскостным расстоянием и обозначается буквой d. На рис. 2 приведены проекции нескольких семейств плоскостей и указаны соответствующие межплоскостные расстояния. Пространственное расположение плоскостей данного семейства однозначно определяется расположением одной из параллельных плоскостей. Для определенности берут плоскость семейства, ближайшую к началу координат, но не проходящую через начало координат.
В общем случае такая плоскость отсекает на координатных осях отрезки, величина которых может быть выражена в долях элементарных трансляций. Пусть, например, плоскость отсекает на осях отрезки a/h, b/k, c/l (рис.3).
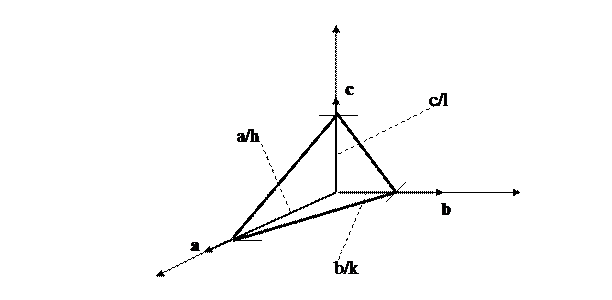
Рис. 3. К определению индексов плоскости.
Числа h, k, l, характеризующие наклон плоскости по отношению к основным кристаллографическим осям, являются координатами или индексами данной плоскости и, в то же время, –индексами всего семейства параллельных плоскостей.
Индексы плоскостей принято заключать в круглые скобки – (h k l), причем запятые между h,k,l  не ставятся.
не ставятся.
По имени ученого, впервые предложившего такое определение индексов, они называются индексами Миллера.
Если h, k, l являются дробными, то индексами семейства служат целые числа – числители, приведенных к общему знаменателю, дробей. Так, например, если плоскости отсекают по оси x отрезок a/2, по оси y – 2b/3, а по оси z –1, т.е. h=2, k=3/2, l=1, то индексы Миллера в данном случае есть (432).
Если плоскость отсекает на какой- либо оси отрезок в отрицательном направлении, то над соответствующим индексом ставится знак минус (например, ( 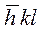 )).
)).
Если плоскости семейства параллельны какому-либо из основных кристаллографических направлений, т.е. пересекают его в бесконечности, то соответствующий индекс Миллера равен 0 (например, плоскости семейства (hk0) параллельны оси z).
Если плоскости семейства параллельны какой-либо из координатных плоскостей, т.е. параллельны двум основным осям, то два соответствующих индекса равны 0 (так плоскости (00l) параллельны координатной плоскости xy, а (0k0) – плоскости xz).
Легко убедится, что семейства плоскостей с небольшими межплоскостными расстояниями dhkl имеют сравнительно большие индексы Миллера, а семейства с большими dhkl - относительно малые индексы.
Число узлов, приходящихся на единицу площади плоскости данного семейства, называется ретикулярной плотностью. Если рассматривать только такие семейства плоскостей, каждое из которых содержат все узлы решетки, то системы с наибольшими dhkl будут содержать плоскости с наибольшей ретикулярной плотностью (т.к. число атомов в данном кристалле постоянно). 
Геометрический смысл индексов плоскости (hkl) ясен из уравнения плоскости в отрезках, представленного в декартовых координатах X,Y,Z:
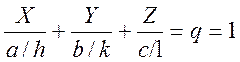 (4)
(4)
Уравнение (4) есть уравнение первой от начало координат плоскости семейства hkl.
 1. 4. Элементарная ячейка кристалла.
1. 4. Элементарная ячейка кристалла.
Параллелепипед, построенный на трёх основных векторах 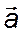
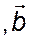 и
и 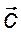 , называется элементарной ячейкой кристалла.Поскольку основные векторы являются периодами идентичности в трёх основных кристаллографических направлениях, то элементарная ячейка является тем наименьшим «кирпичиком» структуры, путём многократного параллельного переноса которого вдоль трёх основных осей может быть мысленно построен весь кристалл.
, называется элементарной ячейкой кристалла.Поскольку основные векторы являются периодами идентичности в трёх основных кристаллографических направлениях, то элементарная ячейка является тем наименьшим «кирпичиком» структуры, путём многократного параллельного переноса которого вдоль трёх основных осей может быть мысленно построен весь кристалл.
Доказано, что наиболее рациональным для описания атомной пространственной структуры данного кристалла является выбор основных векторов в соответствии со следующими правилами:
1) симметрия, получающаяся при этом элементарной ячейки, должна соответствовать симметрии решетки;
2) число равных ребер и число равных углов элементарного параллелепипеда должно быть по возможности максимальным;
3) при наличии прямых углов число их должно быть также по возможности максимальным.
При соблюдении первых трех условий объем элементарной ячейки должен быть минимальным из всех возможных.
Величины трех ребер элементарной ячейки (a, b, c), в совокупности с величинами трех углов между осями параллелепипеда ( 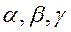 ) называются параметрами элементарной ячейки. Элементарная ячейка называется простой или примитивной, если атомы (ионы) находятся только в ее вершинах. В сложных элементарных ячейках атомы могут находиться, кроме вершин, на гранях и в объеме. Число атомов, приходящихся на одну элементарную ячейку, в кристаллах химических соединений может изменяться от одного (рис.4а) до десятков, сотен и даже тысяч (последнее - в случае сложных органических соединений).
) называются параметрами элементарной ячейки. Элементарная ячейка называется простой или примитивной, если атомы (ионы) находятся только в ее вершинах. В сложных элементарных ячейках атомы могут находиться, кроме вершин, на гранях и в объеме. Число атомов, приходящихся на одну элементарную ячейку, в кристаллах химических соединений может изменяться от одного (рис.4а) до десятков, сотен и даже тысяч (последнее - в случае сложных органических соединений).
В непримитивных элементарных ячейках узлы, в которые возможен переход из данного узла путем элементарных трансляций, называется трансляционно-идентичными (в таких узлах обязательно должны располагаться атомы одного сорта), а узлы, в которые нельзя попасть путем таких трансляций – трансляционно-неидентичными между собой. Трансляционно- неидентичные атомы, приходящиеся на одну элементарную ячейку, называют базисными атомами, а совокупность координат всех базисных атомов (узлов)- базисом элементарной ячейки. Базис примитивной ячейки – (000) (рис. 4а). Базис ячейки, у которой, кроме атомов в вершинах имеется атом вцентре объема (так называемая объемноцентрированная ячейка на рис. 4б) -



 0 0 0
0 0 0
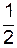
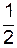
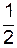
Базис ячейки, у которой кроме атомов в вершине, имеются атомы в центре каждой грани (т.н. гранецентрированная ячейка), рис.4в-
 |  |
0 0 0
0 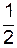
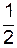
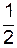 0
0 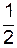
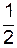
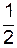 0
0

Рис.4. Типы элементарных ячеек:
а) примитивная; б) объемноцентрированная; в) гранецентрированная
1. 5. Элементы симметрии.
Симметрия – способность твердого тела совмещаться с самим собой в результате его движения или воображаемых операций над ним. Рассмотрим три основных операции симметрии.
1. Ось симметрии n-ого порядка. Если тело совмещается с самим собой при повороте на угол 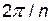 вокруг оси, то ось называется осью симметрии n-ого порядка.
вокруг оси, то ось называется осью симметрии n-ого порядка.
2. Плоскость симметрии. Если тело совмещается с самим в результате зеркального отражения его точек в некоторой плоскости, то эта плоскость называется плоскостью симметрии.
3.Центр симметрии (инверсии). Если тело совмещается с самим собой при инверсии относительно некоторой точки, то эта точка называется центром симметрии или центром инверсии.
Комбинации этих основных элементов симметрии приводит к сложным элементам симметрии, например, к инверсионному повороту, т. е. комбинации поворота с одновременной инверсией и т.п.
При преобразовании рассмотренных выше элементов симметрии хотя бы одна точка остается неподвижной. Поэтому они называются точечными элементами симметрии. В твердых телах и геометрических фигурах возможны оси симметрии любых порядков, в кристаллах же возможны только оси симметрии 1, 2, 3, 4, 6. В них невозможны оси симметрии 5-ого и порядка выше 6-ого. Это ограничение обусловлено тем, что кристаллическое вещество – бесконечная система материальных частиц, симметрично повторяющихся в пространстве. Такие симметричные бесконечные ряды, сетки, решетки, непрерывно заполняющие пространство, несовместимы с осями 5, 7, и других более высоких порядков.
Cингонии.
По характеру симметрии кристалла и его пространственной решетки, от которой зависят, в частности, соотношения между параметрами элементарной ячейки, все виды пространственных решеток могут быть отнесены к одной из семи систем или сингоний (триклинной, моноклинной, ромбической, ромбоэдрической, гексагональной, тетрагональной, кубической).
Характерные особенности каждой сингонии и формулы, связывающие величины межплоскостных расстояний с индексами соответствующих семейств плоскостей и параметрами решетки, т.н. квадратичные формы, приведены в табл.№1.
Пространственные решетки, в которых атомы расположены только в вершинах элементарных ячеек (узлах), называются простыми или примитивными. Решетки, в которых атомы расположены не только по вершинам, но и внутри ячеек и на их гранях, называются сложными.
Очевидно, химические соединения не могут иметь простые решетки, Среди химических элементов простую (ромбоэдрическую) решетку имеет одна лишь ртуть. Для металлов характерны сложные плотно упакованные решетки. Наиболее распространены среди металлов решетки объемноцентрированная кубическая ( ОЦК), гранецентрированная кубическая (ГЦК) и компактная гексагональная. Помимо атомов в вершинах (узлах), ячейки этих решеток содержат по одному атому: ОЦК – в центре куба, ГЦК – в центрах каждой из шести граней куба, гексагональная компактная – в центре двух трехгранных призм, образующих параллелепипед.
В простой пространственной решетке на долю одной элементарной ячейки приходится всего один атом (каждой из восьми атомов, расположенных в вершинах, принадлежит одновременно восьми соседним ячейкам 8 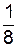 =1).
=1).
В cложных пространственных решетках на долю элементарной ячейки приходится несколько атомов. Сложные решетки можно рассматривать как совокупность нескольких простых решеток, вставленных друг в друга. Число этих простых решеток равно числу атомов, приходящихся на долю сложной элементарной ячейки.
Сложные решетки называются иногда решетками с базисом. Под базисом решетки понимают совокупность координат атомов, входящих в сложную элементарную ячейку, выраженных в осевых единицах.
В таблице № 2 приведены данные о базисе основных решеток, коэффициенте заполнения 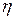 (отношения объема, занимаемого атомами, к объему элементарной ячейки) и координационном числе – к.ч. (число ближайших соседних атомов в решетке).
(отношения объема, занимаемого атомами, к объему элементарной ячейки) и координационном числе – к.ч. (число ближайших соседних атомов в решетке).
(110). В кубической сингонии их называют плоскостями ромбического додекаэдра.
Плоскости, пересекающие одну ось и параллельные двум другим (например, осям Y и Z) обозначают (100) и называют в кубической решетке плоскостями куба.
Индексы направлений. Под кристаллографическими индексами направления понимают три целых взаимно простых числа, пропорциональных координатам любого атома, лежащего на данном направлении, измеренным в осевых единицах.
При установлении кристаллографических индексов данного направления его необходимо перенести параллельно самому себе в начало координат.
Для кубической сингонии индексы направления 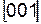 , перпендикулярного к плоскостям (001), численно равны индексам этой плоскости. Так индексы оси X равны
, перпендикулярного к плоскостям (001), численно равны индексам этой плоскости. Так индексы оси X равны 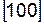 , а индексы плоскости, перпендикулярной оси Y, равны (010).
, а индексы плоскости, перпендикулярной оси Y, равны (010).
Угол между двумя направлениями в кубической сингонии с индексами 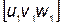 и
и 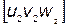 может быть найден из уравнения
может быть найден из уравнения
cosj = 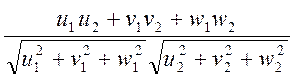
 (5)
(5)
Совокупность семейств плоскостей, параллельных одному направлению 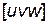 в решетке, называется кристаллографической зоной, а само направление осью зоны.
в решетке, называется кристаллографической зоной, а само направление осью зоны.
Между индексами оси зоны 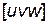 и индексами (hkl) плоскостей, входящих в данную зону, имеет место следующая зависимость
и индексами (hkl) плоскостей, входящих в данную зону, имеет место следующая зависимость
hu+kv +lv =0 (6)
Уравнение (6) определяет таким образом условие зональности.
Каждое семейство плоскостей с индексами (hkl) характеризуется также своим межплоскостным расстоянием d, то есть расстоянием между двумя соседними параллельными плоскостями
В случае сложной решетки, состоящей как бы из нескольких простых, межплоскостное расстояние равно расстоянию между соседними параллельными плоскостями одной простой решетки. Так в случае ОЦК межплоскостное расстояние для плоскостей (100) равно периоду решетки а, но не а/2.
Между индексами (hkl), величиной d и периодами решетки а,b,c, существует зависимость, различная для каждой сингонии.
Приводим те из них, которые часто используются в рентгеноструктурном анализе поликристаллов.
Все кристаллографически идентичные семейства плоскостей образуют совокупность плоскостей, обозначаемую фигурными скобками {hkl}.
Так в кубической сингонии совокупность плоскостей куба {100} содержит шесть кристаллографически идентичных семейств плоскостей  ,
, 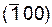 ,
, 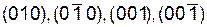 . Если, например, путем различных операций симметрии повернуть (001) в любое из остальных четырех семейств плоскостей, то новое положение решетки совпадет с начальным. В этом и заключается кристаллографическая идентичность.
. Если, например, путем различных операций симметрии повернуть (001) в любое из остальных четырех семейств плоскостей, то новое положение решетки совпадет с начальным. В этом и заключается кристаллографическая идентичность.
Важнейшим признаком кристаллографически идентичных плоскостей является то, что они обладают одинаковым межплоскостным расстоянием. Поэтому количество кристаллографически идентичных плоскостей (семейств плоскостей) для любой совокупности равно числу возможных перестановок местами и знаками индексов, входящих в данную совокупность, не изменяющих величины межплоскостного расстояния.
В качестве примера рассмотрим те же шесть плоскостей. В случаи кубической сингонии согласно (7) для всех шести семейств плоскостей куба d=a,и они входят в одну совокупность.
В случае тетрагональной сингонии (см. формулу (8)) эти шесть плоскостей разбиваются на две совокупности. В одну из них {100} входят четыре плоскости: (100), 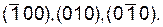 Для них d=a.
Для них d=a.
Во вторую совокупность {001} входят две плоскости (001) и 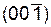 . Для них d¹a.
. Для них d¹a.
Приводим количество кристаллографически идентичных плоскостей P для совокупностей с разными индексами в кубической сингонии (таблица 4).
В геометрической кристаллографии, изучающей формы кристаллов и многогранников, рассмотренному представлению о совокупности кристаллографически идентичных плоскостей соответствует представление о простой форме. Под простой формой понимают совокупность граней, которые может быть выведена из одной посредством разных операций симметрии.
То же можно сказать и о совокупности кристаллографически идентичных семейств плоскостей. Рассмотрим шлиф поликристаллического образца металла с кубической решеткой, в которой зерна ориентированы беспорядочно. В различных зернах параллельными плоскостями шлифа окажутся разные кристаллографические семейства плоскостей. Если теперь каким либо методом (фигур травления, фигур давления и др.) определить эти плоскости, то окажется (при большом числе зерен), что число зерен, ориентированных параллельно плоскости шлифа плоскостям (100), (110), (111) будет относиться как P 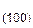 : P
: P 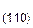 : P
: P 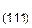 =6: 12: 8.
=6: 12: 8.
При наличии преимущественной ориентировки (текстуры) это отношение будет нарушено.
Дата добавления: 2021-02-19; просмотров: 916;











