Метод замены плоскостей проекций

Для упрощения решения метрических, а также некоторых позиционных задач могут применяться методы, позволяющие переходить от задания фигур общих положений к частным. Эти методы основываются на двух принципах:

1) замещение системы плоскостей проекций на новую систему плоскостей, в которой неподвижный геометрический объект занимает какое-либо частное положение (способ замены плоскостей проекций);

2) перемещение геометрического объекта в пространстве таким образом, чтобы он занял какое-либо частное положение в неподвижной системе плоскостей проекций (способ вращения).

В зависимости от расположения оси в пространстве, вокруг которой вращается геометрический объект, различают следующие виды способа вращения:

1) вращение вокруг линии уровня;

2) вращение вокруг проецирующей прямой;

3) плоско-параллельное перемещение.

Эти способы преобразования включают в себя четыре основные задачи начертательной геометрии:

1) Преобразование комплексного чертежа таким образом, чтобы прямая общего положения стала линией уровня.

2) Преобразование комплексного чертежа таким образом, чтобы линия уровня стала проецирующей прямой.

3) Преобразование комплексного чертежа таким образом, чтобы плоскость общего положения стала проецирующей плоскостью уровня.

4) Преобразование комплексного чертежа таким образом, чтобы проецирующая плоскость стала плоскостью уровня.

Сущность этого метода заключается в том, что проецируемый объект не изменяет своего положения в пространстве, а заменяется система плоскостей проекций. Может быть заменена одна, две и более плоскостей. Замена производится до тех пор, пока геометрический объект не займет частное положение относительно новой плоскости проекций. При этом новая плоскость должна быть перпендикулярна оставшейся «старой» плоскости проекций.

Возьмем точку А, расположенную в ортогональной системе плоскостей проекций , и повернем вокруг нее горизонтальную плоскость проекций P₁ в положение , получив таким образом новую ортогональную систему плоскостей проекций . При этом должно соблюдаться следующее условие:

Расстояние от точки до «старой» плоскости проекций в новой системе плоскостей проекций должно остаться неизменным (рис.8.1).

Рисунок 8.1. Модель и КЧ преобразования точки

1 основная задача. Преобразованием прямой общего положения в прямую уровня можно определить (рис.8.2):

- натуральную длину отрезка;

- углы наклона прямой к плоскостям проекций.

Рисунок 8.2. Преобразование прямой

2 основная задача. С помощью преобразования прямой уровня в проецирующую прямую можно найти:

-расстояние между точкой и прямой;

-расстояние между параллельными или скрещивающимися прямыми и т.п.

3 основная задача. Преобразованием плоскости общего положения в проецирующую плоскость можно определить (рис.8.3):

- расстояние от точки до плоскости или расстояние между параллельными плоскостями;

- углы наклона плоскости к плоскостям проекций.

4 основная задача. Преобразованием проецирующей плоскости в плоскость уровня можно найти:

- натуральную величину плоской фигуры;

- угол между пересекающимися прямыми;

- центр описанной или вписанной окружности;

- построить биссектрису угла и т.п.

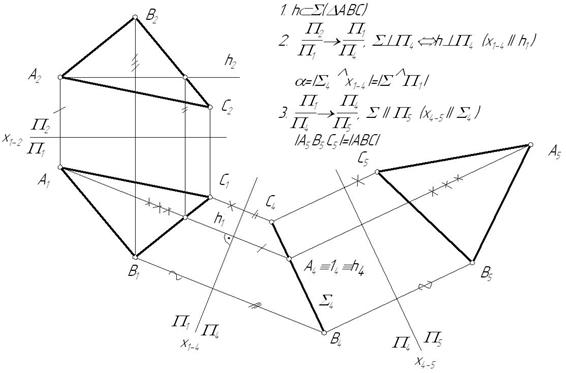
Рисунок 8.3. Преобразование плоскости