Оценка точности формул интегрирования

При приближенном интегрировании функций необходимо знать погрешность, с которой получено приближенное значение интеграла, так как без нее полученный результат не представляет ценности. Из геометрического смысла интеграла ясно, что каждая из рассмотренных формул дает результат тем точнее, чем больше n, и что наиболее точной является формула Симпсона, а наименее точными – формулы правых и левых прямоугольников. Однако увеличение nведет к возрастанию объема вычислительной работы, что нежелательно, особенно при ручных вычислениях на ЭКВМ.

В математическом анализе выводят формулы для оценки погрешности 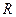приближенного интегрирования, имеющие вид для

1) формулы средних прямоугольников

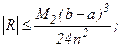(6.14)

2) формулы трапеций:

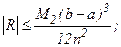(6.15)

3) формулы Симпсона:

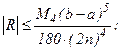(6.16)

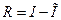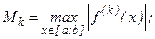
где ; 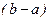– длина отрезка интегрирования; 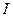– точное значение интеграла; 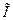– приближенное значение интеграла, вычисленное по формуле средних прямоугольников, трапеций или Симпсона.

Пользуясь этими формулами, можно по заранее заданной точности 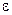приближенно вычислить необходимое число отрезков 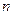. Ясно, что формулы (6.14), (6.15) и (6.16) неприменимы, если функция 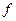задана графически или таблично. Практически ими редко пользуются и при аналитическом задании функции 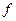, так как вычисление производных 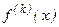и их оценка обычно весьма трудоемки. Кроме того, промежуточные результаты (ординаты, их суммирование и т. п.) вычисляются приближенно и с округлением, поэтому в окончательном результате надо учитывать и эти погрешности.

При вычислениях на ЭВМ для оценки погрешности интегрирования используется так называемый метод автоматического выбора шага интегрирования для достижения заданной точности. Алгоритм этого метода состоит из следующих этапов:

1. Выбирается начальное значение nи вычисляется шаг интегрирования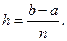

2. Вычисляется значение интеграла 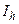для этого начального шага .

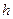3. Затем шаг 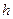уменьшается в два раза 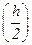, и для него вычисляется значение интеграла .

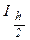4. Сравниваются полученные два значения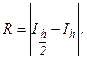

5. Полученная погрешность 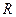сравнивается с заранее заданной точностью 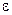. Если 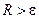, то точность не достигнута, и величине 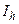присваивается более точное значение 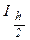, после чего повторяются этапы 3, 4 и 5 до выполнения условия .

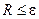6. При выполнении условия 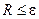за искомое значение интеграла 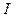принимается последнее значение величины .

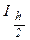Этот алгоритм реализуется в стандартной подпрограмме вычисления значения интеграла по формуле Симпсона с заранее заданной точностью 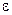. Она включается в библиотеку стандартных подпрограмм (БСП) современных вычислительных машин. Причем число делений заданного отрезка интегрирования выбирается из ряда чисел, начиная с 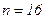, то есть 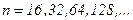, представляющих собой степени основания двоичной системы счисления ( 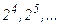). Такой выбор обусловлен точностью преобразования этих чисел из десятичной системы счисления в двоичную.

При вычислениях на ЭВМ по формуле Симпсона для достижения заданной точности в три – четыре значащие цифры, как правило, табулируют функцию при 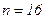(17 ординат) и вычисляют интеграл 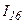, затем вычисляют интеграл с удвоенным шагом 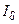, делая выборку значений функции через одно и оставляя в промежуточных вычислениях до шести значащих цифр.

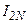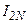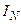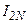В качестве приближенного значения интеграла принимают значение , руководствуясь при этом таким практическим правилом: считается, что в , точных значащих цифр на одну больше, чем совпадающих цифр в , и . Погрешность 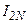не превосходит числа

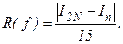
Если приближенное значение интеграла вычисляют по формулам средних прямоугольников или трапеций с двойным пересчетом (то есть с вычислением 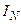, и 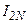), то для оценки погрешности 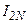приближенного интегрирования получают

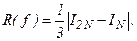
Поскольку вычисление и оценка производных 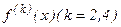обычно трудоемки, то в формулах (14) - (16) вместо производных часто используют отношения соответствующих конечных разностей к шагу интегрирования, то есть полагают

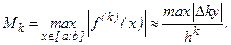
Аналогично оценивают погрешность квадратурных формул и в тех случаях, когда подынтегральная функция задана таблично или графически.

Контрольные вопросы

1. Что такое квадратурная формула? Что такое узлы и веса?

2. Какие квадратурные формулы Вы знаете? Каково их общее название?

3. С какой целью и как интерполируют подынтегральные функции?

4. Как вычисляются и какими свойствами обладают коэффициенты Котеса?

5. Приведете иллюстрации использования формулы прямоугольников (срединных, левых, правых).

6. Сравните по ошибке интегрирования частные случаи формулы Ньютона-Котеса.

7. Сравните по ошибке интегрирования формулы прямоугольников (срединных, левых, правых).

8. Численное интегрирование, постановка задачи.

9. Оценка точности формул интегрирования.

10. В чем состоит суть методов численного интегрирования функций?

11. Охарактеризуйте метод трапеций.

12. Опишите формулу Симпсона.

13. Приведите оценку погрешности для каждого из методов на частичном отрезке и на всем интервале интегрирования.

14. Проведите сравнение формул численного интегрирования по точности на основании остаточных членов формул.

15. Как оценивается погрешности приближенного вычисления интегралов по правилу Рунге?