Формула прямоугольников

Для вычисления приближенного значения интеграла

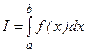отрезок 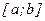делят на 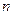равных частей точками 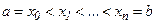так, что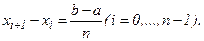

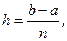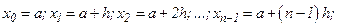
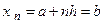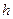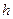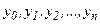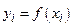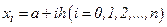Тогда длина каждого частичного отрезка а точки разбиения образуют арифметическую прогрессию с разностью . Эти точки называют узлами, а - шагом интегрирования. Затем в узлах вычисляют ординаты то есть для . На частичных отрезках 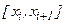строят прямоугольники (рисунок 6.2.1 – 6.2.2), высота которых равна значению 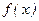в какой-либо точке каждого частичного отрезка.

Тогда произведение 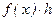дает площадь частичного прямоугольника, а сумма таких произведений дает площадь ступенчатой фигуры, представляющую собой приближенное значение интеграла.

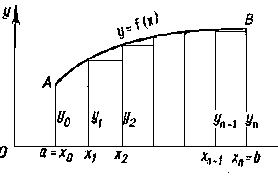
Рисунок 6.2.1 – Построение прямоугольников на каждом частичном отрезке

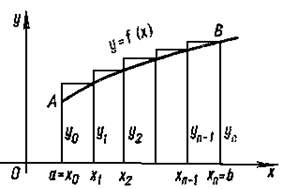
Рисунок 6.2.2 - Построение прямоугольников на каждом частичном отрезке

Если 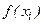вычисляют в левых концах отрезков 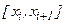, то получают формулу левых прямоугольников вида:

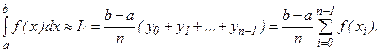
Если 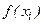вычисляют в правых концах отрезков 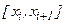, то получают формулу правых прямоугольников вида:

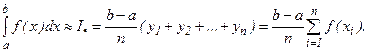
Если же функцию 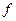вычисляют в точках 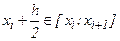, то получают формулу средних прямоугольников вида:

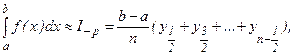(6.7)

где

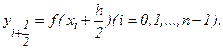
В том частном случае, когда функция f монотонно возрастает на 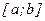, величина 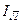дает значение интеграла 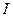с недостатком (ломанная вписана в криволинейную трапецию), а величина 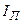- с избытком (ломаная описана). Их среднее арифметическое значение дает более точный результат:

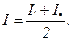
Формула трапеций

Формулу трапеций получают аналогично формуле прямоугольников, но на каждом частичном отрезке строится трапеция (рис.6.3.1).

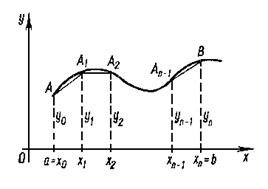
Рисунок 6.3.1 – Построение трапеции на каждом частичном отрезке

Тогда площадь криволинейной трапеции приближенно равна площади фигуры, ограниченной ломаной линией

. Площади частичных трапеций:

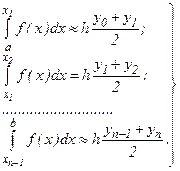(6.8)

Суммируя равенства (6.8), получим формулу трапеций:

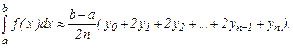(6.9)

Формула Симпсона

Для построения формулы Симпсона предварительно рассмотрим такую задачу: вычислить площадь криволинейной трапеции, ограниченной сверху графиком параболы 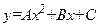, слева прямой 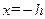, справа прямой 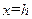и снизу отрезком 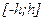. Пусть парабола проходит через три точки (рис.6.4.1): 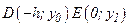и 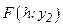, причем 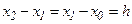. Следовательно, .

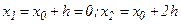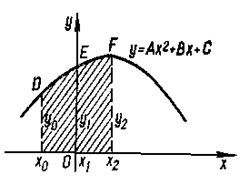
Рисунок 6.4.1 – Построение формулы Симпсона

Тогда площадь S равна интегралу:

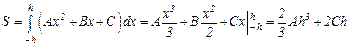(6.11)

Выразим эту площадь через 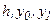и 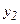. Для этого вычислим коэффициенты параболы 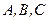. Из условия, что парабола проходит через точк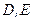и и 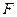, имеем:

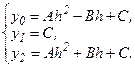
Решая эту систему, получаем: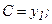

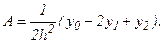
Подставляя эти значения и в (6.11), получаем искомую площадь

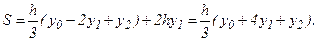(6.12)

Перейдем теперь к выводу формулы Симпсона для вычисления интеграла

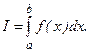
Для этого отрезок интегрирования 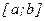разобьем на 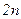равных частей длиной 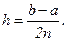В точках деления (рис.6.4.2)

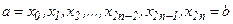вычисляем значения подынтегральной функции 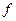: 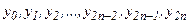, где .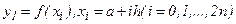

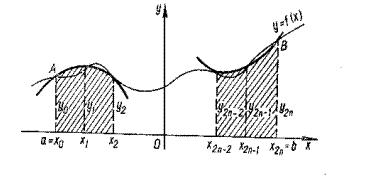
Рисунок 6.4.2 – Вычисление значения подынтегральной функции в точках деления

На отрезке 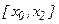подынтегральную функцию заменяем параболой, проходящей через точк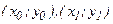и и 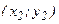, и для вычисления приближенного значения интеграла от 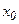до 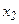воспользуемся формулой (6.12). Тогда (на рис. 6.4.2 заштрихованная площадь):

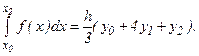
Аналогично находим:

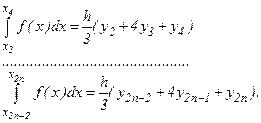
Сложив полученные равенства, имеем:

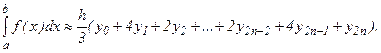
Или

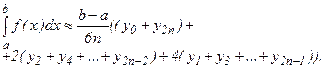(6.13)

Формула (6.13) называется обобщенной формулой Симпсона или формулой парабол, так как при ее выводе график подынтегральной функции на частичном отрезке длины 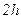заменяется дугой параболы.