Алгоритм метода наискорейшего спуска

При заданной точке x алгоритм наискорейшего спуска заключается в реализации линейного поиска вдоль направления - 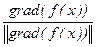или, что то же самое, вдоль направления - .

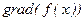Начальный этап. Пусть 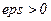- константа остановки. Выбрать начальную точку x1, положить k=1 и перейти к основному этапу.

Основной этап. Если 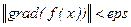, то остановиться; в противном случае положить 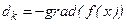и найти 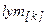- оптимальное решение задачи минимизации 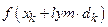при . Положить 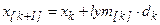, заменить 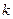на 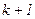и повторить основной этап.

Контрольные вопросы

1. В чем суть метода Хука и Дживса?

2. Метод координатного спуска и его реализация для функций многих переменных?

3. Метод наискорейшего координатного спуска, в чем его суть?

4. Метод градиентного спуска?

5. В чем отличие многомерных методов поиска с использованием и без использования производной?

Лекция 6. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

План

6.1 Постановка задачи

6.2 Формула прямоугольников

6.3 Формула трапеций

6.4 Формула Симпсона

6.5 Формула Симпсона

Постановка задачи

Вычисление скалярных аддитивных величин обычно сводится к суммированию бесконечно большого числа беcконечно малых слагаемых такого вида:

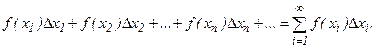
Например, если значение функции 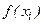считать проекцией силы на ось ОХ, а малую величину 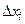- «элементарным» перемещением некоторой массы под действием этой силы, то произведение 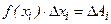даст «элементарную» работу 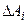силы 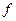на малом перемещении 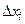. Работа силы 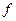на всем перемещении массы по свойству аддитивности будет равна сумме «элементарных» работ

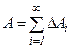
Но так как физически не представляется возможным просуммировать бесконечно много слагаемых 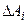, то, ограничиваясь 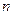слагаемыми, можно получить приближенное значение данной величины:

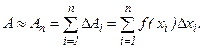
Точное значение таких величин выражается с помощью предельного перехода, в результате которого получают интеграл:

где 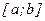- отрезок, на котором задана функция .

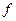Определение понятия интеграла и его геометрическую интерпретацию.

Пусть на конечном отрезке 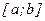задано непрерывную функцию 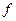(рисунок 6.1.1), причем 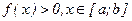и .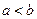

1. Разобьем отрезок 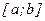произвольным образом на 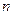частичных отрезков точками:

.

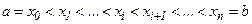2. Обозначим длину каждого частичного отрезка через

.

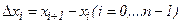3. Выберем произвольно в каждом частичном отрезке точку

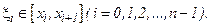
4. Составим произведения значений функции 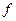в точке 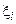на длину 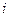-го отрезка, т.е. .

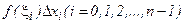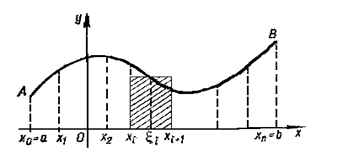
Рисунок 6.1.1 – Геометрическая интерпретация интеграла

Геометрически это произведение дает площадь «элементарного» 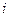-го прямоугольника, заштрихованного на рисунке 6.1.1.

5. Просуммируем полученные произведения:

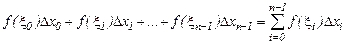(6.1)

Полученную таким образом сумму (6.1) называют интегральной суммой. Геометрически эта сумма дает площадь всех 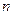«элементарных» прямоугольников, то есть площадь ступенчатой фигуры. Отметим, что интегральных сумм (6.1) можно построить бесконечно много в силу того, что при их построении допускается два произвола: разбиение отрезка 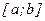на части точками 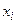и выбор точек на каждом из частичных отрезков .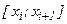

6. Выполним предельный переход при условии, что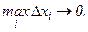

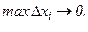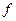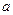Если при интегральная сумма (6.1) имеет конечный предел, то этот предел называется интегралом функции от до 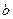и обозначается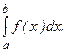

Следовательно, 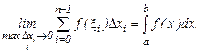(6.2)

Таким образом, интегралом функции 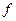на отрезке интегрировании от 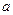до 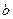называется предел интегральных сумм при условии, что максимальная длина частичных отрезков стремится к нулю, следовательно, число их неограниченно возрастает, то есть .

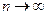В силу непрерывности функции 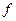площадь ступенчатой фигуры (рис.6.1.1) при большом 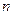«почти совпадает» с площадью криволинейной трапеции 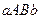, а при 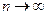интеграл (6.2) и дает точное значение площади 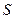криволинейной трапеции с основанием 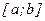, ограниченной сверху графиком функции :

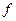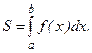
Можно доказать, что если функции 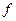непрерывна на отрезке 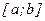, то предел (6.2) существует.

Формула (6.2) непригодна для точного вычисления интеграла, так как операция вычисления предела интегральной суммы практически не всегда легко выполнима.

Для вычисления точного значения интеграла (6.2) используют понятие первообразной функции. Пусть подынтегральная функция 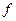непрерывна на отрезке 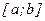и известна ее первообразная 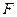, то есть такая функция, что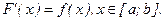

Тогда интеграл (6.2) может быть вычислен по формуле Ньютона-Лейбница

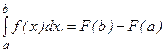, (6.3)

как приращение первообразной функции 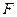на отрезке .

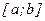Кроме того, можно доказать, что если существует интеграл (6.3), то одной из первообразных функций на 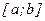для подынтегральной функции является интеграл с переменным верхним пределом 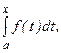так как

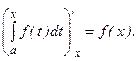
Таким образом, если мы умеем найти первообразную функцию, то можем вычислить также и интеграл.

Однако очень часто нахождение первообразной функции затруднительно, громоздко или вообще невыполнимо в элементарных функциях. Тогда задача вычисления точного значения интеграла по формуле Ньютона-Лейбница (6.3) оказывается неразрешимой. Класс функций 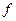, для которых первообразная 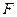выражается через элементарные функции, весьма узок, а , значит, и формула (6.3) не всегда пригодна для практики. Например, не выражается в элементарных функциях первообразная для функции

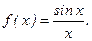
В таких случаях действие интегрирования порождает новый класс неэлементарных функций. Так, для приведенной выше функции получаем (по определению) неэлементарную функцию

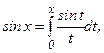(6.4)

которую называют интегральным синусом. Значение этой функции, например, при 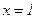равно 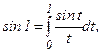то есть значением функции является интеграл, не выражающийся в элементарных функциях, а не число в явном виде, что было бы практически значительно удобнее. Кроме того, на практике часто подынтегральная функция 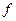задается графически или таблично, тогда само понятие первообразной теряет смысл и формула Ньютона - Лейбница, несмотря на ее большое теоретическое и практическое значение, опять «не работает».

Таким образом, приходится иметь дело с интегралами, которые не выражаются в элементарных функциях. В этих случаях незаменимое значение приобретает приближенное интегрирование. Для приближенного интегрирования функций разработано много численных методов. Сущность этих методов состоит в том, что значение интеграла вычисляется приближенно по формулам вида

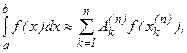(6.5)

в которых используется ряд значений подынтегральной функции. Формулу (и сумму) вида (6.5) называют квадратурной. Действительные числа 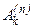и 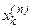называют соответственно коэффициентами и узлами квадратурной формулы (6.5). Величину

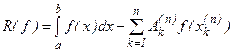(6.6)

называют остаточным членом (или погрешностью) квадратурной формулы (6.5).

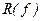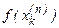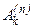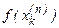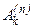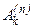Заменяя интеграл квадратурной суммой, мы пренебрегаем остаточным членом (это погрешность метода). Выполняя вычисления по формуле (6.5), всегда оперируют не с точными, а с приближенными значениями подынтегральной функции и коэффициентов . Погрешность, с которой заданы значения и , переносится и на квадратурную сумму (это так называемая неустранимая погрешность формулы (6.5)). Если - точные числа (с такими формулами мы будем иметь дело), а значения 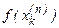вычислены с погрешностью 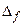, то значение квадратурной суммы будет вычислено с неустранимой погрешностью

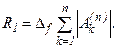
При нахождении квадратурной суммы все промежуточные вычисления рекомендуется проводить с 1 - 2 запасными цифрами. Это дает возможность пренебрегать погрешностями округлений в промежуточных вычислениях. Однако при отбрасывании запасных цифр в конечном результате необходимо учитывать заключительную погрешность округления 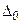. Таким образом, суммарная погрешность численного интегрирования функций 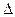представляет собой сумму трех указанных выше погрешностей: .

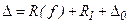Геометрически общий подход к решению задачи приближенного интегрирования функций состоит в том, что в криволинейную трапецию, площадь которой равна искомому значению интеграла, вписывают (или описывают) «частичные» прямоугольники, трапеции или параболы, находят их площади, а затем суммируют. В результате получают приближенное значение искомого интеграла, так как при этом график функции 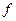заменяют некоторой ломаной линией. В соответствии с выбором геометрической фигуры для вычисления интеграла различают формулы: прямоугольников, трапеций, парабол (Симпсона). Для получения этих формул отрезок интегрирования 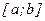делят на частичные отрезки равной длины.