Лекция 8. РЕШЕНИЕ ЗАДАЧ ИНТЕРПОЛЯЦИИ И ЭКСТРАПОЛЯЦИИ

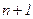Пусть на интервале заданы опорных (узловых) точек 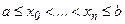. Пусть, кроме того, заданы 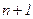действительных чисел 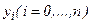(например, как значения функции в узловых точках). Под задачей интерполяции понимают нахождение многочлена 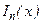степени не больше 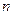такой, что 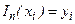для .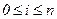

Интерполяцию обычно применяют тогда, когда относительно 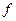известны только дискретные значения функции 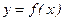, и, чтобы вычислить другие ее значения между узловыми точками (интерполяция) или за отрезком узловых точек (экстраполяция), ее приближают многочленом 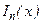, причем .

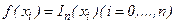Всегда существует только один интерполяционный многочлен, который может быть представлен в различной форме.

Форма Лагранжа: ;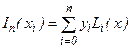

.

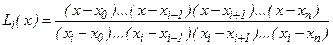Нетрудно видеть, что 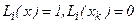при 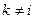, и, следовательно, .

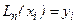Форма Ньютона: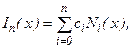

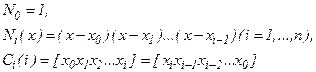
где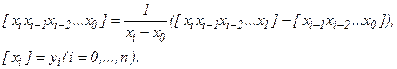

Выражение 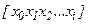называется разделенной разностью. Для определения многочлена в форме Ньютона применяют разностную схему или схему спуска (см. литературу).

Пример 1 Нахождение интерполяционного многочлена.

Пусть после опыта получены следующие пары: .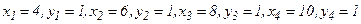

Многочлен Ньютона:

.

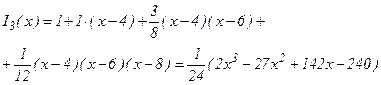Многочлен Лагранжа:

.

Часто применяют равноотстоящие узловые точки (узловые точки, расположенные на равном расстоянии друг от друга):

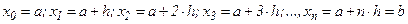, т.е. .

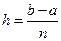В этом случае разделенные разности выражаются через простые разности:

,

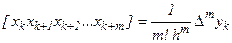где .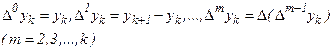

Разностная схема упрощается. Формула Ньютона принимает вид:

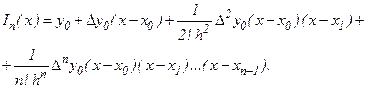
Контрольные вопросы

1. Как ставится задача интерполяции?

2. Какие виды интерполяции вы знаете?

3. В чем суть и геометрический смысл линейной интерполяции?

4. Какова схема построения интерполяционного многочлена в форме Лагранжа?

5. Как выглядит оценка точности при интерполировании многочленом?

6. Что означают понятия интерполяции и экстраполяции?

7. Каков результат решения задачи интерполяции и экстраполяции?

8. Как изменяется качество интерполяции при увеличении числа узлов интерполяции?

9. Сравните методы интерполяции по объему вычислений, т.е. по затратам машинного времени.

10. Методы решение задач интерполяции и экстраполяции.

11. Понятия интерполяции и экстраполяции.

12. Интерполяционный полином Лагранжа.

13. Первый интерполяционный полином Ньютона.

14. Второй интерполяционный полином Ньютона.

15. Какую функцию называют аппроксимирующей?

16. Охарактеризуйте интерполяционную формулу Лагранжа.

17. Приведите интерполяционные формулы Ньютона и оценку остаточного члена для каждой из формул.

ЗАКЛЮЧЕНИЕ

В результате изучения данного курса студент должен получить основные навыки программирования, изучить наиболее распространенные методы приближенных вычислений. Здесь ставится задача дать фундаментальную подготовку в области профессионального программирования. В большинстве случаев для решения задач обработки эксперимента и математического моделирования процессов уже существуют готовые программные комплексы. Однако, студенты должны иметь ясное представление об основных методах приближенных вычислений и границах их применимости. Это позволит, во-первых, выбирать подходящую для решения конкретной задачи программу, а во-вторых, правильно интерпретировать получаемые результаты.

Рабочая программа учебной дисциплины рассчитана на 43 часа аудиторных занятий и 47 часов отводится на самостоятельное изучение курса. В связи с этим для самостоятельного изучения предлагаются следующие темы:

Алгоритмы нахождения суммы числовых и функциональных рядов (8часов).

Общие сведения, типы рядов. Определение способов вычисления. Ряды: гармоничный, Фурье, степенной, Тейлора, функциональный. Действия над рядами: комбинация рядов, группировки членов ряда, перестановка членов ряда, перемножение рядов. Классификация функциональных рядов или числовых рядов в зависимости от методов вычисления суммы ряда. Вычисление тригонометрических функций с помощью рядов.

Численные методы решения систем уравнений (6 часов).

Прямые методы решения СЛАУ. Методы прогонки. Нормы и обусловленность матрицы линейной системы. Итерационные методы решения линейных систем: метод Якоби. Метод верхней релаксации. Вычисление определителя и обратной матрицы. Нахождение собственных значений матрицы.

Решение оптимизационных задач ( 10 часов)

Поиск экстремума функции нескольких переменных. Метод Нелдера - Мида. Квазиньютоновськи методы. Решение задач оптимизации при наличии ограничений. Метод штрафных функций. Численное интегрирование . ( 88 часов )

Квадратурные формулы Гаусса. Методы численного интегрирования несобственных, кратных интегралов, интегралов с переменной границей интегрирования. Методы интегрирования быстро осциллирующих функций. Метод Монте - Карло.

Интерполяция и экстраполяция ( 13 часов )

Интерполяционный полином Эрмита. Кусково - многочленов интерполяция функций. Интерполяция сплайнами. В- сплайны. Полиномы Чебышева. Тригонометрическая интерполяция. Дискретное преобразование Фурье. Быстрое преобразование Фурье. Принципы аппроксимации производных. Метод наименьших квадратов. Сглаживание экспериментальных данных.

Численное дифференцирование ( 8 часов )

Принципы аппроксимации производных. Структура формул численного дифференцирования. Погрешность аппроксимации производных.

СПИСОК ИСТОЧНИКОВ

1. Бахвалов Н. С. Численные методы: Учеб. пособие./ Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. - М.: Наука, 1987. – 600с.

2. Гулин И. А. Численные методы./ Гулин И. А., Самарский А. А. - М.: Наука, 1989.408с.

3. Березин И. С. Методы вычислений./ Березин И. С. , Жидков Н. П. - В 2–х т. М., 1959, т.1.– 464 с. т.2 – 602 с.

4. Бахвалов Н. С. Численные методы в задачах и упражнениях. / Бахвалов Н. С., Лапин А. В., Чижонков Е. В. - М., Высшая школа, 2000. – 190 с.

5. Каханер Д. Численные методы и программное обеспечение. / Каханер Д., Моулер К., Неш С. – М.:Мир, 2001. – 575с.

6. Ильина В. А. Численные методы для физиков-теоретиков. / Ильина В. А., Силаев П. К. – Москва-Ижевск: ИКИ, 2003. – т 1,2.

7. Фельдман Л. П.. Чисельні методи в інформатиці. / Фельдман Л. П., Петренко А. І., Дмитрієва О. А. – К.: Видавнича група BHV, 2006. - 480 c.

8. Волков Б. И. Математический практикум для физиков. М.: Изд-во МГУ, 1981. – 104 с.

9. Гаврилюк І. П. Збірник задач з методів обчислень. / Гаврилюк І. П., Копистира М. П., Макаров В. Л., Москальков М. М.. - К.:ВЦ «Київський університет», 2004. – т 1,2.

10. Шмидский Я. К. Mathematica 5. Самоучитель. - М.: Издательский дом «Вильямс», 2004. – 529 с.

11. Электронная библиотека. Режим доступа: http://ecnmx.ru.

12. Математическая энциклопедия. Режим доступа: http://dic.academic.ru/contents.nsf/enc_mathematics.

13. Свободная энциклопедия. Режим доступа: http://uk.wikipedia.org/wiki/Теорія_керування.

14. Элементы вычислительной математики - образовательный портал. Режим доступа: http://dl.sumdu.edu.ua/e-pub/tutor08/index.html.

15. Научная библиотека. Режим доступа: http://sernam.ru/.