Лабораторная работа №3
Численные методы решения систем нелинейных уравнений
Цель работы:сформировать у студентов представления о методах решения систем нелинейных уравнений, привить умения составлять и применять алгоритмы для решения таких систем уравнений, выработать навыки в использовании программных средств для решения систем уравнений.
Метод Ньютона
Пример 3.1.
Решить систему двух нелинейных уравнений
 x+3lg(x) – y2 = 0
x+3lg(x) – y2 = 0
2x2 – xy – 5x + 1=0
методом Ньютона.
Решение.
1. Зададим координатную сетку и вычислим значения
координат х и у в узлах сетки (рис. 3.1).
2. Построим график функции и карты линий уровня (рис. 3.2)
(на которых наглядно видно, что данная система имеет
решение, и причем единственное) с использованием панели
Graph (рис. 3.3.).
n = 100
xmin = 1 xmax = 5 ymax = 5 ymin = 1
i = 0…n j = 0..n
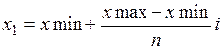
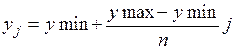
g(x,y) = 2x2 – xy – 5x +1
Mi,j = g(xi, yj) Ni,j = q(xi, yj)
Рис. 3.1.Задание координатной сетки
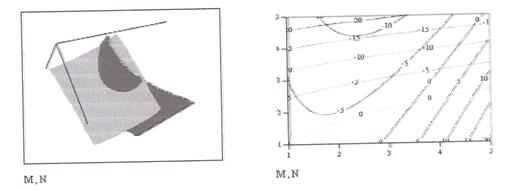
Рис. 3.2.График функции и карта линий уровня
Рис. 3.3.ПанельGraph
Точки пересечения линий одинакового уровня дают решение данной системы уравнений.
4. Зададим начальное приближение переменных:
х = 3.4 у = 2.2
5. Зададим функцию, содержащую решение системы уравнений
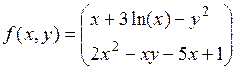
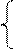 x + 3lg(x) – y2 = 0
x + 3lg(x) – y2 = 0
2x2 – xy – 5x + 1 = 0
Рис. 3.4.Вектор-функция, задающая систему уравнений
6. Зададим функцию (рис. 3.5.), реализующую метод Ньютона
(функция F возвращает таблицу, содержащую значения
координат х, у на каждом шаге итерации и соответствующие
значения координат вектор - функции).

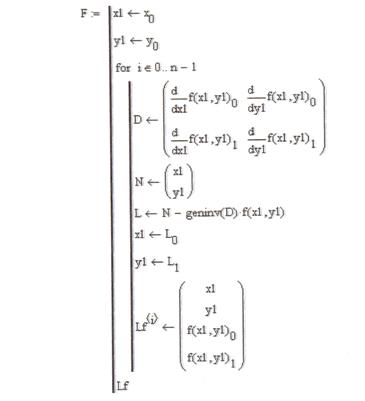
Рис. 3.5.Функция, возвращающая решение системы методом Ньютона
Запустив программу, получим итерационную последовательность (рис. 3.6), которая показывает, как находятся приближения. Здесь две первые строки – это значения х и у соответственно, а последние две строки – значения данных функций при найденных значениях х и у. В ноль функции обращаются на седьмом шаге. Значит, решением будет являться пара чисел х = 3,487 и
у = 2,262.
F =
| 8,502 | 5,365 | 3,986 | 3,545 | 3,488 | 3,487 | 3,487 | 3,487 | |
| 5,573 | 3,475 | 2,578 | 2,298 | 2,262 | 2,262 | 2,262 | 2,262 | |
| -19,771 | -4,522 | -0,857 | -0,087 | 1,452·10-3 | 4,367· 10-7 | 997· 10-14 | ||
| 55,679 | 13,1 | 2,568 | 0,265 | 4,435·10-3 | 1,333· 10-6 | 137· 10-13 |
Рис. 3.6.Итерационная последовательность, полученная для решения системы нелинейных уравнений по методу Ньютона
7. Визуализируем итерационный процесс (рис. 3.7), транспонируя для этого полученную матрицу F:
F1 = FТ
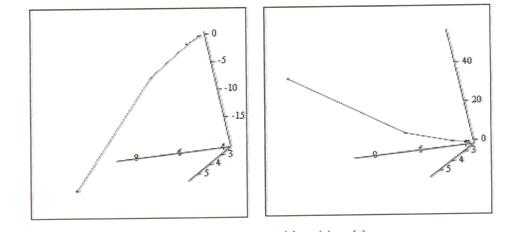
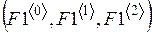
Рис. 3.7.Визуализация итерационного процесса
8. Проверяем решение системы нелинейных уравнений с помощью блока Given...Minerr (рис.3.8).
х = 3,4 у = 2,2 Given
х + 3log(x) – y2 = 0
2x2 – xy – 5x + 1 = 0
Z = Minerr (x, y
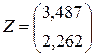
Рис.3.8.Проверка численного решения с помощью
встроенных функций пакета Mathcad
Вопросы по теме


Дата добавления: 2021-09-07; просмотров: 578;











