Задание к лабораторной работе №4
Задание 4.1.
Найти приближенное значение интеграла заданной функции
f(x) на отрезке [a, b] по формулам трапеций, Симпсона,
прямоугольников, Монте – Карло при делении отрезка на
1000 равных частей, произвести оценку погрешности
методом интегрирования и сравнить точность полученных
результатов: составить функцию, возвращающую значение
интеграла на основе формулы метода Монте – Карло.
Сравнить результаты, полученные разными методами.
Таблица 4.1. Варианты заданий для выполнения самостоятельной
работы
| № | F( x) | [a, b] |
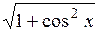
| [0; 3] | |
| sin(2x2 + 1) | [0; 1] | |
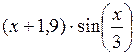
| [1; 2] | |
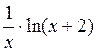
| [2; 3] | |
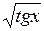
| [0; 0,5] | |
| 2,6 · x2 · ln x | [1,2; 2,2] | |
| (x2 + 1) · sin (x – 0,5) | [0,5; 1,5] | |
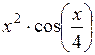
| [2; 3] | |
| 3x + ln x | [1; 2] | |
| 3x2 + tg x | [-0,5; 0,5] | |
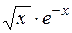
| [0,1; 1,1] | |
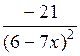
| [-2; 0] | |
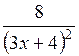
| [0; 1] | |
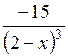
| [3; 5] | |
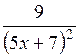
| [2; 3] | |
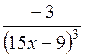
| [-1; 0] | |
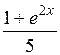
| [0; 3] | |
| ex·sin(x2) | [0; 5] | |
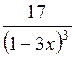
| [-3; -1] | |
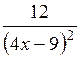
| [0; 1] | |
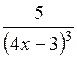
| [4; 5] | |
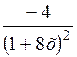
| [0; 3] | |
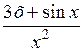
| [0,1; 1,1] | |
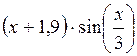
| [1; 2] | |
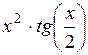
| [1,5; 2,5] | |
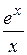
| [1; 7] | |
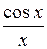
| 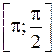
| |
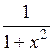
| [0; 1] | |
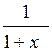
| [0; 9] | |
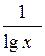
| [4; 10] | |
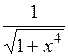
| [0; 6] | |
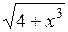
| [0; 3] | |
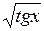
| 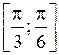
| |
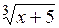
| [0; 8] | |
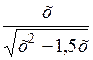
| [2; 5] | |
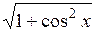
| [0; π] | |
| (x – 5)2 (10 – x) | [0; 10] | |
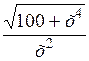
| [2; 4] | |
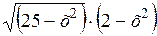
| [0; 2] | |
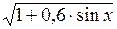
| [0; π / 2] |

Лабораторная работа №5
Решение обыкновенных дифференциальных уравнений
Цель работы: сформировать у студентов представление о применении ДУ в различных областях; привить умения решать задачу Коши для ДУ у' = f(x, y) на отрезке [ a, b] при заданном начальном условии у0 = f(x0) методами Пикара, Эйлера, Рунге – Кутты, Адамса; развить навыки проверки полученных результатов с помощью прикладных программ.
Метод Пикара
Пример 5.1.
Решить задачу Коши для ДУ 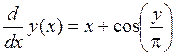 на отрезке [1,7; 2,7] при заданном НУ: у(1,7) = 5,3 и шаге интегрирования h = 0,1 методом Пикара с шагом h.
на отрезке [1,7; 2,7] при заданном НУ: у(1,7) = 5,3 и шаге интегрирования h = 0,1 методом Пикара с шагом h.
В отчете представить: ход работы, программу – функцию, погрешность, графическую иллюстрацию решения.
Решение.
1. Вводим данные (рис. 5.1)
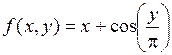
a = 1,7 b = 2,7
h = 0,1 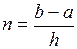
y0 = 5,3 i = 0..n
Рис.5.1.Задание исходных данных
2. Задаем функцию, возвращающую значения первой производной по переменной у (рис.5.2).
f derive(y) = 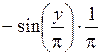
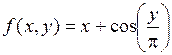
Рис.5.2.Функция, возвращающая значение первой производной функции
3. Составим функцию, возвращающую решение ДУ методом
Пикара. Здесь: f – исходнаяфункция; f deriv –
Производная функции по у; a,b – концы отрезка; h – шаг; у0 –
начальное значение переменной у.
4. Найдем решение ДУ методом Пикара (рис. 5.3).
fnPikan(fn, fn derive, a, b, h, y0)= 
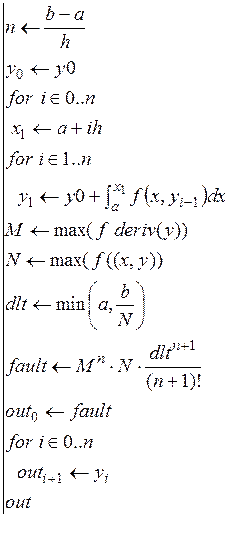
Рис. 5.3.Задание функции, возвращающей решение ДУ
методом Пикара (файл fnPikar.mcd)
fnPikar(f, f derive, a, b, 0.1, y0) =
| 7,78457519486·10-11 | |
| 5,3 | |
| 5,46340155616 | |
| 5,62650688007 | |
| 5,78947945853 | |
| 5,95251650231 | |
| 6,11584391144 | |
| 6,27971330675 | |
| 6,44440084325 | |
| 6,61020759752 | |
| 6,77746140952 | |
| 6,94652015221 |
Рис. 5.4.Нахождение численного решения ДУ методом Пикара
Дата добавления: 2021-09-07; просмотров: 595;











