Метод Рунге – Кутты

На практике наиболее часто используют метод Рунге – Кутты четвертого порядка.

Пример 5.3.

Решить задачу Коши для ДУ 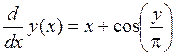на отрезке [1,7; 2,7] при заданном НУ у(1,7) = 5,3 и шаге интегрирования h = 0,1 методом Рунге – Кутты четвертого порядка с шагом h и 2h.

В отчете представить: ход работы, программу функцию, погрешность, графическую иллюстрацию решения и оценку погрешности приближения.

Решение.

1. Вводим данные задачи (рис. 5.9).

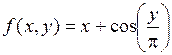a = 1,7 b = 2,7

h = 0,1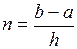

y0 = 5,3

i = 0..n

Рис.5.9.Задание исходных данных

2. Составим функцию, возвращающую решение ДУ первого порядка методом Рунге – Кутты. Здесь: fn – заданная функция; a, b – концы отрезка; h – шаг; y0 – начальное значение функции.

3. Найдем решение ДУ первого порядка, используя встроенные функции Mathcad (рис. 5.10).

RK h = fnRungeKutta(f, a, b, h, y0)

RK 2h = fnRungeKutta(f, a, b, 2h, y0)

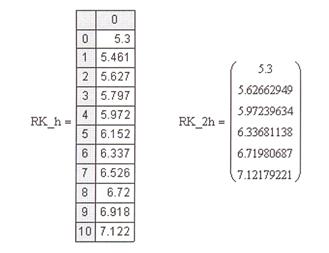
Рис. 5.10.Листинг функции, возвращающей численное

решение ДУ методом Рунге–Кутты

Метод Адамса

Пример 5.4.

Решить задачу Коши для ДУ 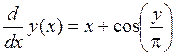на отрезке [1,7; 2,7] при заданном НУ у(1,7) = 5,3 и шаге интегрирования h = 0,1 методом Адамса с шагом h.

В отчете представить: ручной счет, программу – функцию, погрешность, графическую иллюстрацию решения и оценку погрешности приближения.

Решение.

1. Найдем первые четыре числа по формуле Рунге–Кутты (рис. 5.11).

y_i = fnRungeKutta(f, a, b, h, y0)_i

Рис. 5.11.Вычисление первых четырех значений численного решения по формуле Рунге–Кутты

2. Составим функцию, реализующую метод Адамса (рис. 2.10.3). Здесь a, b – концы отрезка; y1 – начальное значение функции; h – шаг.

Рис. 5.12.Функция, возвращающая численное решение

ДУ методом Адамса

3. Графическая иллюстрация решения ДУ разными методами представлена на рис. 5.13.

Рис. 5.13.Визуализация решения ДУ разными методами

Вопросы по теме

1. Что значит – решить задачу Коши для ДУ первого порядка?

2. Графическая интерпретация численного решения ДУ.

3. Какие существуют методы решения ДУ в зависимости от

формы представления решения?

4. В чем заключается суть принципа сжимающих

отображений?

5. Рекуррентная формула метода Пикара.

6. В чем заключается суть метода ломаных Эйлера?

7. Применение, каких формул позволяет получить значения

искомой функции по методу Эйлера?

8. Графическая интерпретация метода Эйлера и

усовершенствованного метода Эйлера. В чем их отличие?

9. В чем заключается суть метода Рунге–Кутты?

10. Как определить количество верных цифр в числе,

являющемся решением ДУ методом Эйлера,

усовершенствованного метода Эйлера, Пикара, Рунге–

Кутты?