Метод Эйлера и его модификации

Пример 5.2.

Решить задачу Коши для ДУ 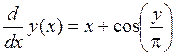на отрезке [1,7; 2,7] при заданном НУ: у(1,7) = 5,3 и шаге интегрирования h = 0,1 методом Эйлера и усовершенствованным методом Эйлера с шагами h и h/2.

В отчете представить: ход работы, программу функцию, погрешность, графическую иллюстрацию решения и оценку погрешности приближения.

Решение.

Ход решения задачи по методу Эйлера приведен на рис. 5.5 – 5.7.

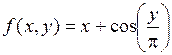а = 1,7 b = 2,7 у0 = 5,3

h = 0,1 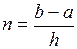n = 10

i = 0..n

y₀ = y0 x_i = a + ih h2 = 0,05

Рис5.5.Фрагмент рабочего листа Маthcad с решением

уравнения методом Эйлера с шагом h и h/2 и графической

визуализацией метода Эйлера.

1. Составим программу, реализующую метод Эйлера(рис.

5.6).

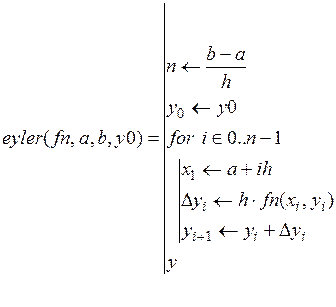
Рис.5.6.Листинг программы, реализующий метод Эйлера

2. Получим решение ДУ методом Эйлера(рис. 5.7.).

ES h = eyler(f, a, b, h, y0)

ES h2 = eyler(f, a, b, 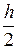, y0)

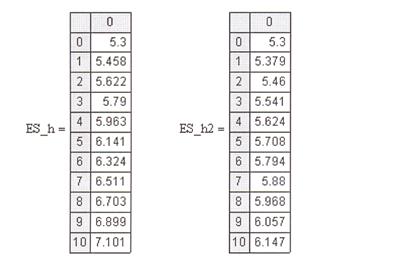
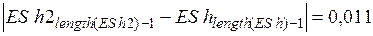
Рис. 5.7.Нахождение численного решения ДУ методом Эйлера

Примечание

Функцию, возвращающую решение ДУ усовершенствованным методом Эйлера, составить самостоятельно.

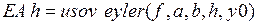
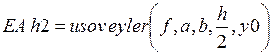
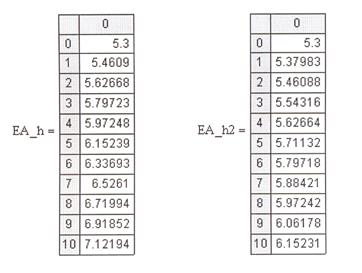
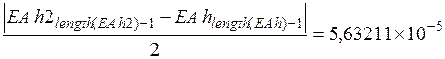
Рис. 5.8.Решение ДУ усовершенствованным методом

Эйлера с шагами h и h/2