Метод Монте – Карло

Пример 3.4.

Вычислить приближенное значение интеграла 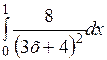, используя метод Монте – Карло, при п = 1000000.

Решение.

Реализация метода Монте – Карло для вычисления интеграла представлена на рис. 4.5.

Сравнивая точное и численное значение интегралов находим, что абсолютная погрешность равна 1,6·10^-4.

a = 0 b = 1 n = 1000000

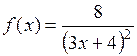
i = 0..n

x_i = a + (b – a) · md(1)

I = 0,285550681

Рис. 4.5.Ход решения задачи на нахождение значения

интеграла с помощью метода Монте – Карло

Вопросы по теме

1. В каком случае используется численное интегрирование?

2. Постановка задачи численного интегрирования.

3. Какие существуют методы интегрирования функции?

4. Графическая интерпретация метода трапеций.

5. Как оценить погрешность метода трапеций?

6. Графическая интерпретация метода Симпсона.

7. Как оценить погрешность метода Симпсона?

8. Графическая интерпретация метода прямоугольников.

9. Как оценить погрешность метода прямоугольников?

10. Чем отличаются формулы метода трапеций и метода

Симпсона?

11. Как влияет на точность численного интегрирования

величина шага h?

12. Чем отличается вычисление погрешности метода

трапеций и Симпсона?

13. Основная идея метода Монте – Карло.

14. Графическая интерпретация метода Монте – Карло.