Задание к лабораторной работе № 5

Задание 5.1.

Решить задачу Коши для ДУ y’ = f(x, y) на отрезке [a, b] при заданном НУ у(а) = с и шаге интегрирования h (исходные параметры заданы в табл. 2.10.1):

1) методом Эйлера и усовершенствованным методом Эйлера с шагом h и h/2;

2) методом Рунге–Кутты с шагом h и 2h;

3) методом Адамса;

4) методом Пикара.

Решение должно содержать: ход работы, программу метода, графическое решение уравнения и оценка погрешности приближения. В числах оставлять 5 цифр после запятой.

Таблица 5.1.Варианты заданий для выполнения самостоятельной работы

№	f(x, y)	[a, b]	y0	h
	3х2 + 0,1ху	[0; 1]	у(0) = 0,2	0,1
	0,185(x2 + cos(0,7x)) + 1,843y	[0,2; 1,2]	у(0,2) = 0,25	0,1
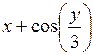
		[1,6; 2,6]	у(1,6) = 4,6	0,1
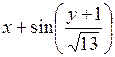
		[0,2; 1,2]	у(0,2) = 1,1	0,1
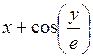
		[1,4; 2,4]	у(1,4) = 2,5	0,1
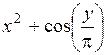
		[1,7; 2,7]	у(1,7) = 5,3	0,1
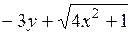
		[2,6; 4,6]	у(2,6) = 3,5	0,2
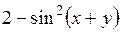
		[2; 3]	у(2) = 2,3	0,1
	1,6 + 0,5y2	[0; 1]	у(0) = 0,3	0,1
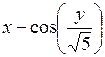
		[1,8; 2,8]	у(1,8) = 2,6	0,1
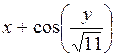
		[2,1; 3,1]	у(2,1) = 2,5	0,1
	e2x + 0,25y2	[0; 0,5]	у(0) = 2,6	0,05
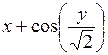
		[- 2; -1]	у(-2) = 3	0,1
	0,133·(x2 + sin(2x)) + 0,872y	[0,2; 1,2]	у(0,2) = 0,25	0,1
	sin(x + y) +1,5	[1,5; 2,5]	у(1,5) = 4,5	0,1
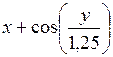
		[0,4; 1,4]	у(0,4) = 0,8	0,1
	2,5x + cos(y + 0,6)	[1; 3]	у(1) = 1,5	0,2
	cos(1,5y +x)2 + 1,4	[1; 2]	у(1) = 1,5	0,1
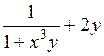
		[1,5; 2]	у(1,5) = 2,1	0,05
	cos y + 3x	[0; 2]	у(0) = 1,3	0,1
	cos(1,5x – y2) – 1,3	[-1; 1]	у(-1) = 0,2	0,2
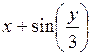
		[1,6; 2,6]	у(1,6) = 4,6	0,1
	e-(y – 1) + 2x	[0; 0,5]	у(0) = 0,3	0,05
	1 + 2y sin x – y2	[1; 2]	у(1) = 0	0,1
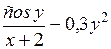
		[0; 1]	у(0) = 0	0,1
	0,166(x2 + sin(1,1x)) + 0,883y	[0,2; 1,2]	у(0,2) = 0,25	0,1
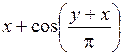
		[1,7; 2,7]	у(1,7) = 5,6	0,1
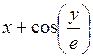
		[1,4; 2,4]	у(1,4) = 2,5	0,1
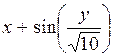
		[0,6; 1,6]	у(0,6) = 0,8	0,1
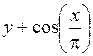
		[1; 2]	у(1) = 5,9	0,1
	1 + 0,8y sin x - 2y2	[0; 1]	у(0) = 0	0,1
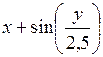
		[0,5; 1,5]	у(0,5) = 1,8	0,1
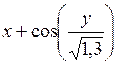
		[1,2; 2,2]	у(1,2) = 1,8	0,1
	1 + 2,2 · sin x + 1,5y2	[0; 1]	у(0) = 0	0,1
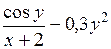
		[0; 1]	у(0) = 0	0,1
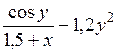
		[0; 1]	у(0) = 0	0,1
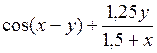
		[0; 1]	у(0) = 0	0,1
	0,2x2 + y2	[0; 1]	у(0) = 0,8	0,1
	x2 + y	[0; 1]	у(0) = 0,4	0,1
	xy + 0,1y2	[0; 1]	у(0) = 0,5	0,1

Литература

Основная литература:

Алексеев Г.В., Вороненко Б.А., Лукин Н.И. Математические методы в

пищевой инженерии: Учебное пособие. – СПб.: «Лань», 2012. – 212 с.

Алексеев Г.В. Математические методы в инженерии: Учеб.-метод. пособие. – СПб.: НИУ ИТМО; ИХиБТ. 2012. – 39 с.

Алексеев Г.В., Холявин И.И. Численное экономико-математическое моделирование и оптимизация: учебное пособие для вузов, ГИЭФПТ, 2011, 211 с.

Макаров Е.Г. Mathcad: Учебный курс. – СПб.: Питер, 2009. - 384 с.

дополнительная литература:

Поршнев С.В.,Беленкова И.В. Численные методы на базе Mathcad. –

СПб.: БХВ-Петербург, 2005. – 464 с.

Агапьев Б.Д., Белов В.Н., Кесаманлы Ф.П., Козловский В.В., Марков С.И. Обработка экспериментальных данных: Учеб. пособие / СПбГТУ. СПб., 2001.

ГореловаГ.В. Теория вероятностей и математическая статистика в примерах и задачах с применением Excel. – М.: Феникс, 2005. – 476 с.

Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий.-М.: Наука, 1976

Асатурян В.И. Теория планирования эксперимента.-М.: Радио и связь, 1983

Бродский В.З. Введение в факторное планирование эксперимента.-М.: Наука, 1976

Демиденко Е.З. Линейная и нелинейная регрессия.-М.: Финансы и статистика, 1981

Красовский Г.И., Филаретов Г.Ф. Планирование эксперимента.-Минск: БГУ, 1982

Маркова Е.В., Лисенков А.Н. Комбинаторные планы в задачах многофакторного эксперимента.-М.: Наука,1979

Фролькис В.А. Линейная и нелинейная оптимизация.-СПб. 2001. 306 с.

Курицкий Б.Я. Поиск оптимальных решений средствами Excel 7.0.-СПб.: BHV,1997,384с

программное обеспечение и Интернет-ресурсы:

http://www.open-mechanics.com/journals - Процессы и аппараты пищевых производств

http://www.spbgunpt.narod.ru/ur_gigm.htm - Механика жидкости и газа, гидравлика и гидравлические машины

http://elibrary.ru/defaultx.asp - научная электронная библиотека «Elibrary»