Задание к лабораторной работе №3

Задание 3.1.

Решить систему двух нелинейных уравнений (табл. 3.1) методом Ньютона.

Таблица 3.1. Варианты заданий для самостоятельной работы

№	Задание	№	Задание
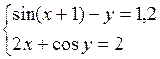
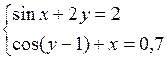
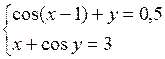
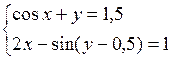
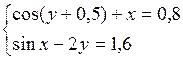
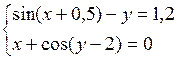
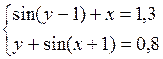
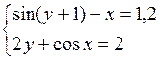
5

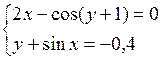
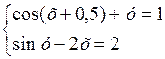
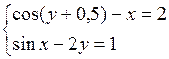
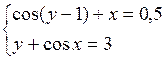
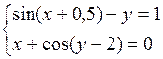
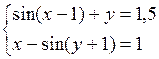
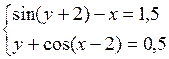
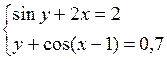
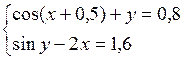
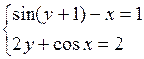
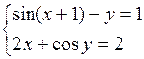
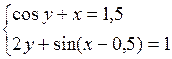
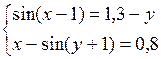
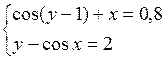
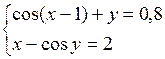
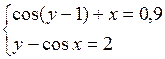
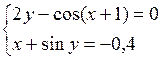
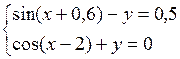
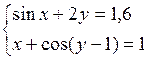
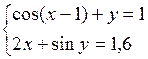
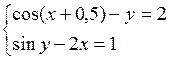
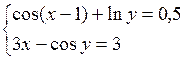
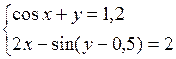
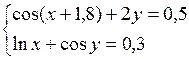
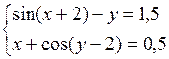
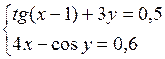
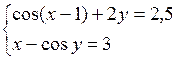
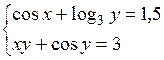
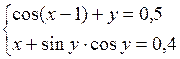
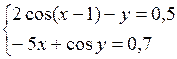
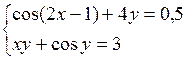
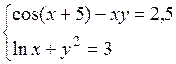
Лабораторная работа№4

Численное интегрирование

Цель работы:ознакомиться с численными методами вычисления определенных интегралов, научиться решать задачи с использованием формулы Симпсона, трапеций, правых и левых прямоугольников, метода Монте-Карло и оценивать погрешность всех перечисленных формул.

Метод прямоугольников

Пример 4.1.

Вычислить приближенное значение интеграла 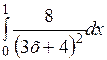, используя формулы левых и правых прямоугольников, при п = 1000.

Решение.

1. Задаем функцию f(x), отрезок [a, b] и функцию

нахождения дифференциалов п – го порядка.

2. Находим значение интеграла заданной функции для

использования его в дальнейшем решении для сравнения

(рис. 4.1).

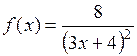
a = 0 b = 1 n = 10C

dif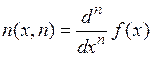

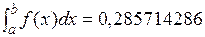
Рис. 4.1.Вычисление точного значения интеграла

Составим функцию, входными параметрами которой являются: а, b – левая и правая границы интервала; п – количество разбиений; char – если имеет значение “left”, то идет подсчет по формуле левых прямоугольников, любое другое – по формуле правых прямоугольников (рис. 4.2).

Погрешность показывает, что полученное значение интеграла верно до третьего знака после запятой.

Рис. 4.2.Функция, возвращающая значение интеграла,

найденного по формулам прямоугольников.

Результаты вычислений по формулам правых и левых прямоугольников:

Integr(a, b, n, “left”) = 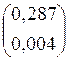Integr(a, b, n, “right) =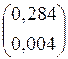

Метод Симпсона

Пример 4.2.

Вычислить приближенное значение интеграла ,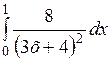

используя общую формулу Симпсона, при n = 1000.

Решение.

Составим функцию, входными параметрами которой являются: a, b – левая и правая границы интервала; n – количество разбиений. Индексы iEven и iUneven обозначают четность и нечетность соответственно (рис. 4.3.).

Simpson(a, b, n) =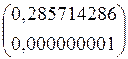

Рис 4.3.Функция, возвращающая значение интеграла

с помощью метода Симпсона

Следовательно, решением будет число, равное 0,285714286. Погрешность показывает, что полученное значение интеграла верно до девятого знака.

Метод трапеций

Пример 4.3.

Вычислить приближенное значение интеграла 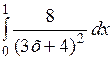, используя формулу трапеций (1.6.16), при п = 1000.

Решение.

Функция, реализующая вычисление интеграла методом трапеций, представлена на рис. 4.4.

Рис.4.4. Функция, возвращающая значение интеграла с

использованием формулы трапеций.