Пропорциональное (усилительное, безинерционное, масштабирующее) звено

<2 3 456 7 8 >

Пропорциональное (усилительное, безинерционное, масштабирующее) звено – это звено, выходной сигнал которого пропорционален входному сигналу:

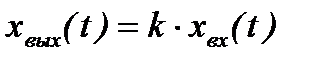где k – коэффициент усиления звена.

Операторное уравнение звена:

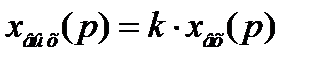
а его передаточная функция:

W(p) = k.

Амплитудно-фазовая характеристика: W(jω)= k.

Соответственно вещественная и мнимая частотные характеристики:

Р(ω) = k, Q(ω) = 0.

Амплитудно- и фазо-частотная характеристики звена:

A(ω)= , .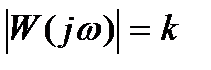

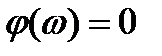Переходная функция звена (рис. 2.7а):

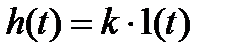Логарифмическая АЧХ звена в соответствии с выражениями (2.41):

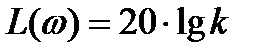Графики логарифмической амплитудно- и фазо-частотной характеристик приведены на рис.2.7б.

Примерами технической реализации пропорциональных звеньев являются потенциометр, полупроводниковый усилитель, зубчатая передача и т.п.

Рис. 2.7а a) Переходная функция пропорционального звена б) Логарифмические амплитудно- и фазо-частотная характеристики пропорционального звена

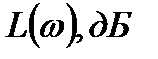
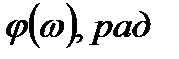
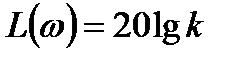
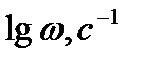
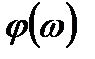
Рис. 2.7б

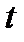
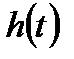
k

Интегрирующее звено

Интегрирующее звено– это звено, выходной сигнал которого пропорционален интегралу по времени от входного сигнала:

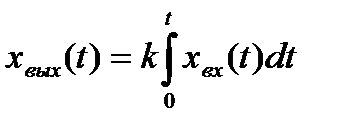
Операторное уравнение, связывающее изображения входного и выходного сигналов звена: 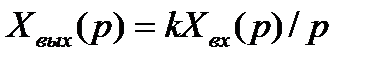, а его передаточная функция:

.

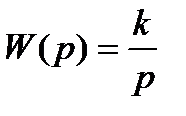Амплитудно-фазовая характеристика звена (рис. 2.8):

W(jω)= .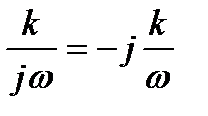

Вещественная и мнимая и частотные характеристики:

Рис. 2.8. АФХ интегрирующего звена

.

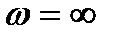
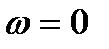
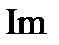
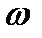
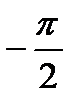
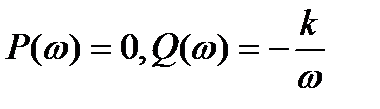Амплитудно- и фазо-частотная характеристики:

A(ω) 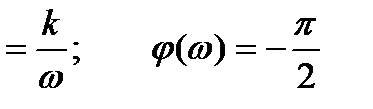. (2.42)

Логарифмическая АЧХ звена с учетом (2.41) и (2.42) описывается выражением:

.

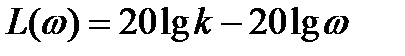Этому уравнению соответствует прямая линия с наклоном -20 дБ/дек. Логарифмическая ФЧХ не зависит от частоты и равна 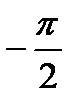. Графики логарифмической амплитудно- и фазочастотной

характеристик приведены на рис. 2.8а.

Выражения для переходной функции и функции веса интегрирующего звена (рис. 2.9б):

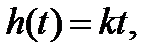w (t) .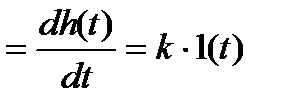

Примеры технической реализации интегрирующего звена: усилитель постоянного тока с большим коэффициентом усиления, в цепь обратной связи которого включен конденсатор.

<2 3 456 7 8 >

Дата добавления: 2017-09-01; просмотров: 1474;