Главное звено машины и его динамическая модель

В рабочих машинах энергия, получаемая от двигателя, преобразуется в механическую работу, идущую на преодоление сил сопротивления, которые возникают при обработке или транспортировке различных материалов.

При изучении динамики машин различают следующие силы сопротивления:

1). Силы полезного (технологического) сопротивления.

Эти силы целиком определяются технологическим процессом, выполняемым машиной (сопротивление металла резанию, вес поднимаемого груза, нагрузка на электрогенератор и т.д.).

2). Силы вредного сопротивления, которые неизбежно возникают в процессе относительного движения частей машины главным образом в виде трения.

Объектами изучения в динамике являются отдельные агрегаты, под которыми понимают совокупность машины двигателя и рабочей машины.

Чтобы изучить движение машины с одной степенью подвижности, достаточно исследовать движение одного ее звена, принятого за главное звено (звено приведения). За главное звено агрегата выгодно выбирать то, которое является общим для машины двигателя и машины рабочей. Для машины двигателя это будут ведомые звенья (кривошипные, коленчатые валы, валы роторов). Для рабочих машин это будут ведущие звенья (главные или приводные валы машин).

а). Закон движения главного звена в форме уравнения кинетической энергии.

Запишем выражение для кинетической энергии агрегата в общем виде.

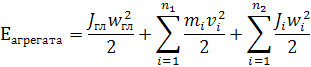
Первый член – кинетическая энергия главного звена.

Второй член – кинетическая энергия поступательного движения.

Третий член – кинетическая энергия вращательно движения.

После преобразования можно получить следующее выражение:

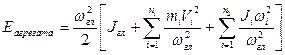Величина, стоящая в квадратных скобках, имеет размерность момента инерции и ее называют приведенным моментом инерции машины. Заменяя скорости звеньев их аналогами, можно записать:

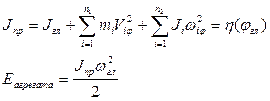Приведенный момент инерции является переменной величиной, зависящей от положения звеньев машины, и функцией угла поворота ее главного звена.

На основании этого выражения можно представить себе, что вместо нескольких подвижных звеньев имеется только одно главное звено с условным моментом инерции J_пр. Движение машины и изменение ее кинетической энергии происходит под действием движущих сил и сил сопротивления. Эти силы могут быть приведены к главному звену в виде двух моментов М_дв и М_сопр, работа которых равна работе всех сил, приложенных к агрегату (рис. 1).

М_сопр

М_дв

J_пр

ω_гл

Рис. 1 Динамика главного звена

С учетом изложенного динамическую модель главного звена можно представить следующим образом:

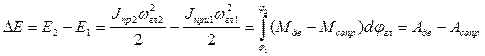(1)

б) Закон движения главного звена в дифференциальной форме

Пусть под действием какого-то момента М_дв0 главное звено вращается равномерно с ω_гл = const. Такое движение называется перманентным. Из (1) следует, что поскольку J_пр – величина переменная, то кинетическая энергия агрегата непрерывно меняется. То есть в данный момент времени моменты М_дв0 и М_сопр не уравновешиваются. За счет разности этих моментов другие звенья машины двигаются с ускорениями. Возникающие при этом силы инерции звеньев приводятся к главному звену в виде некоторого момента инерции М_и0. Согласно принципу Даламбера:

М_дв0 - М_сопр ± М_и0 = 0 (2)

Таким образом, равномерное движение главного звена наступает при условии, что движущий момент М_дв0 целиком расходуется на преодоление М_сопр и на сообщение остальным звеньям ускорения.

Предположим, что движущий момент увеличится на ΔМ_дв. С учетом изложенного ранее эта величина целиком будет потрачена на сообщение главному звену ускорения ε_гл, т.е. на разгон машины.

На такую же величину, но с противоположным знаком изменится приведенный момент от инерционных сил звеньев, т.е. (2) можно переписать в следующем виде:

М_дв0 + ΔМ_дв – М_сопр ± М_и0 – J_прε_гл = 0 (3)

М_дв

Выражение (3) можно решить относительно приведенного момента инерции:

J_прε_гл = М_дв – М_сопр ± М_и0 (4)

Приведенные моменты сил в уравнении движения можно находить с помощью уравнения мгновенных мощностей.