Основные свойства преобразования Лапласа. Операторные уравнения САУ. Передаточные функции линейных звеньев и систем

В общем случае дифференциальное уравнение, связывающее изменение во времени входной и выходной сигналы линеаризованной системы, имеет следующий вид:

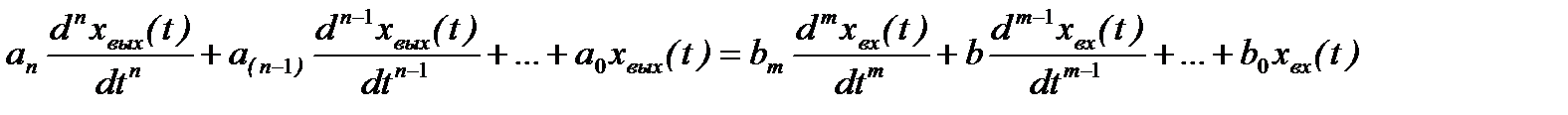
(2.5)

Решение дифференциальных уравнений (2.3) – (2.4) зачастую связа­но со значительными трудностями, а во многих случа­ях, например в следящих системах, не может быть осу­ществлено, так как неизвестно управляющее воздейст­вие. По этим причинам исследование систем ведется косвенными методами, например, базирующимися на операционном преобразовании Лапласа.

Приведем основные сведения о преобразовании Лапласа, которые будут использованы при рассмотрении систем, описываемых линейными дифференциальными уравнениями.

Преобразованием Лапласаназывают интегральное преобразование:

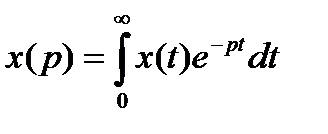, (2.6)

определяющее соответствие между функцией 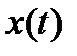вещественного переменного (в рассматриваемой теории – функцией времени 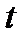) и функцией 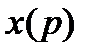комплексного переменного 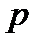. При этом 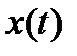называют оригиналом, а 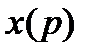– изображениемили изображением по Лапласу. Символическая запись такого преобразования:

= ,

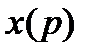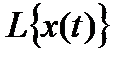где 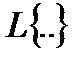– оператор преобразования Лапласа.

Предполагается, что функция времени 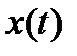, которая подвергается преобразованию Лапласа, обладает следующими свойствами:

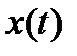· определена и дифференцируема на всей положительной числовой полуоси ;

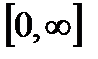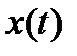· = 0 при ;

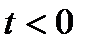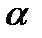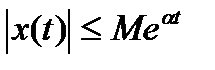· существуют такие числа М и , что при .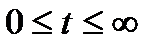

Функции, обладающие указанными тремя свойствами, часто называют функциями-оригиналами.

Соотношение

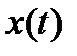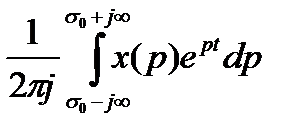= , (2.7)

определяющее по известному изображению его оригинал (в точках непрерывности последнего), называют обратным преобразованием Лапласа. В нем интеграл берется вдоль прямой Re p = 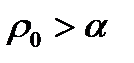. Символически обратное преобразование Лапласа можно записать так:

= ,

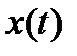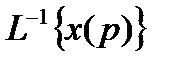где 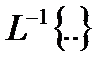– символ обратного преобразования Лапласа.