Апериодическое звено

Подставив в уравнение (1.63) значения b₀ = 0 и a₀ = 0, получим уравнение состояния следующего вида:

a₁ y′(t) + a₂ y(t) = b₁ x(t)(1.75.)

Передаточная функция звена может быть найдена с помощью преобразования по Лапласу и будет иметь вид:

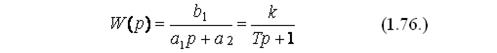
В данном случае Т = a₁ /a₂ – постоянная времени, характеризующая инерционность звена, k – передаточный коэффициент звена, размерность которого определяется отношением размерности выходного параметра к размерности входного. Постоянная времени – время, за которое величина выходного параметра принимает установившееся значение, т.е. с увеличением Т увеличивается инерционность звена. Звено называется апериодическим или инерционным звеном 1-го порядка, т.к. описывается дифференциальным уравнением первого порядка.

При помощи обратного преобразования по Лапласу получим переходную функцию звена, при условии х(t) = 1(t):

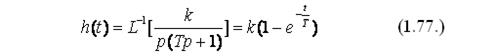
Переходная функция апериодического звена является стабилизирующейся, т.к. при анализе переходной функции можно заметить, что значение величины выходного параметра при постоянном значении величины входного параметра, принимает установившееся значение через определенный промежуток времени. Для получения АФЧХ апериодического звена подставим в выражение (1.76.) jwвместор, и получим:

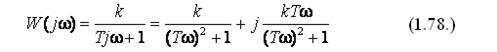
На основании данного выражения определим АЧХ апериодического звена:

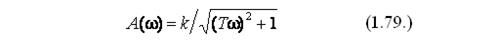
и ФЧХ апериодического звена:

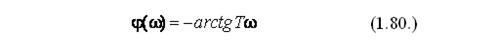
Графическое представление характеристик апериодического звена изображено на рисунке 32.

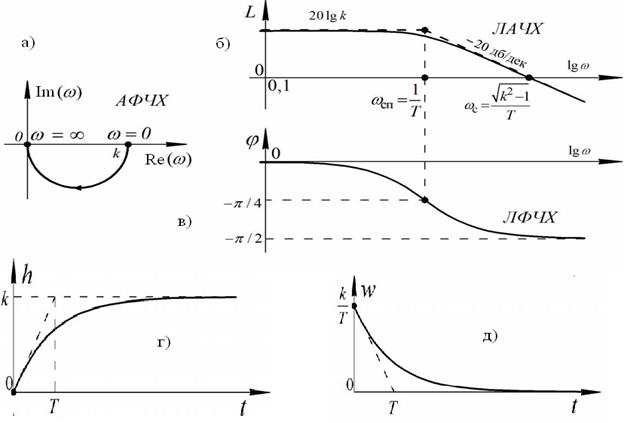
Рис.32. Характеристики апериодического звена: а), б), в) – частотные;

г), д), - временные

Сплошной линией на рисунке 32,б показана кривая, точно соответствующая функции L(ω). На практике чаще всего используют приближенную характеристику данной функции, которая представляет собой ломаную, которая состоит из двух отрезков асимптот. Асимптотические функции являются кусочно-непрерывными функциями, они мало отличаются от действительной функции звена, и используются для упрощения расчетов. При представлении какой-либо функции с помощью асимптотической функции, ошибкой пренебрегают.

Анализируя ЛАЧХ и ЛФЧХ (рисунок 32) нетрудно заметить, что амплитуда выходных колебаний не изменяется до достижения частоты входных колебаний ω_сп, а с увеличением частоты входных колебаний ω > ω_сп, амплитуда выходных колебаний начинает уменьшаться.

На основании проведенного анализа можно сделать вывод, что апериодическое звено является фильтром высоких частот, потому что в основном передает на выход только низкие частоты. С увеличением частоты входных колебаний, их подавление возрастает и увеличивается их сдвиг по фазе. Сдвиг по фазе между входными и выходными колебаниями отрицательный и с увеличением частоты стремится к значению − π /2.

Примерами апериодического звена могут служить: термопара, электродвигатель постоянного тока, четырехполюсник из сопротивления и т.д. Реальная реализация апериодического звена RC-цепочкой представлено на рисунке 33.

Рис.33. Апериодическое звено в виде RC-цепочки