Апериодическое звено

ТИПОВЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ

Обычно система управления состоит из отдельных блоков, каждый из которых описывается уравнениями низкого порядка (чаще всего – первого или второго). Для понимания работы системы в целом желательно хорошо представлять, как ведут себя ее отдельные элементы. Кроме того, при построении ЛАФЧХ сложной системы передаточную функцию разбивают на простейшие сомножители

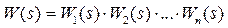
и далее, воспользовавшись свойствами ЛАФЧХ, строят характеристики для всей системы как суммы ЛАЧХ и ЛФЧХ отдельных звеньев.

Усилитель

Звенья, имеющие конечный ненулевой коэффициент усиления постоянного сигнала, то есть W(0) = k ≠ 0, называются позиционными. Это значит, что числитель и знаменатель передаточной функции имеют ненулевые свободные члены (постоянные слагаемые).

Простейшее позиционное звено – идеальный (безынерционный) усилитель. Его передаточная функция 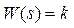. Строго говоря, он не является динамическим звеном, поскольку изменение выхода происходит мгновенно, сразу вслед за изменением входа. При действии на вход единичного ступенчатого сигнала 1(t) (или дельта-функции δ(t)) на выходе будет такой же сигнал, усиленный в k раз, поэтому переходная и импульсная характеристики звена равны

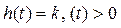и .

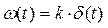Если на вход усилителя действует синусоидальный сигнал, на выходе он усиливается в k раз без изменения фазы, поэтому амплитудная и фазовая частотная характеристики не зависят от частоты входного сигнала

.

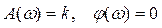Апериодическое звено

Одно из самых часто встречающихся звеньев – апериодическое, которое описывается дифференциальным уравнением

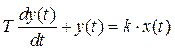, (1)

и имеет передаточную функцию 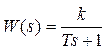. Здесь k – безразмерный коэффициент, а T > 0 – постоянная, которая называется постоянной времени звена. Постоянная времени – размерная величина, она измеряется в секундах и характеризует инерционность объекта, то есть скорость его реакции на изменение входного сигнала.

Переходная и весовая функции апериодического звена

,

.

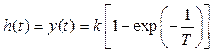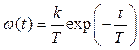Они показаны на рисунке

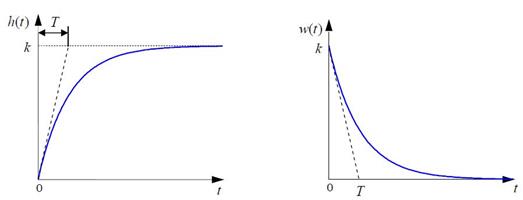
Рисунок 4.1 – Графики переходной и весовой функций апериодического звена первого порядка

Предельное значение переходной характеристики равно k , а касательная к ней в точке t = 0 пересекается с линией установившегося значения при t = T. Переходная и импульсная характеристики выходят на установившееся значение (с ошибкой не более 5%) примерно за время 3T. Эти факты позволяют определять постоянную времени экспериментально, по переходной характеристике звена.

Частотная характеристика определяется выражением

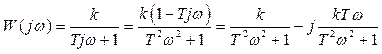. (2)

Для каждой частоты ω значение W(jω) – это точка на комплексной плоскости. При изменении ω от 0 до ∞ получается кривая, которая называется годографом Найквиста (диаграммой Найквиста). В данном случае можно показать, что частотная характеристика – это полуокружность с центром в точке (0,5k; 0) радиуса 0,5k . Годограф начинается (на нулевой частоте) в точке (k; 0) и заканчивается в начале координат (при ω →∞).

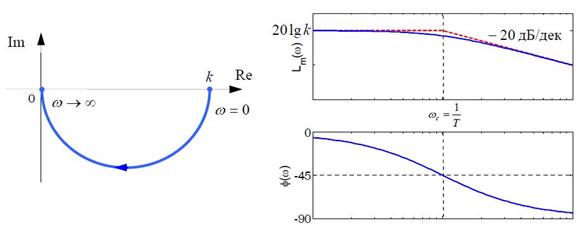
Рисунок 4.2 – Годограф Найквиста апериодического звена первого порядка и асимптотическая ЛАЧХ

Асимптотическая ЛАЧХ этого звена образована двумя прямыми, которые пересекаются на сопрягающей частоте 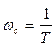. На низких частотах она имеет нулевой наклон (так как звено позиционное), причем в этой области .

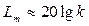На высоких частотах наклон ЛАЧХ равен −20 дБ/дек, так как степень знаменателя передаточной функции на единицу больше степени ее числителя. Фазовая характеристика меняется от 0 до − 90° , причем на сопрягающей частоте ω_с она равна − 45° .

Поскольку ЛАЧХ уменьшается на высоких частотах, апериодическое звено подавляет высокочастотные шумы, то есть обладает свойством фильтра низких частот.