Апериодическое звено первого порядка

Апериодическое звено первого порядка– это звено, выходной сигнал которого связан с входным сигналом следующим дифференциальным уравнением:

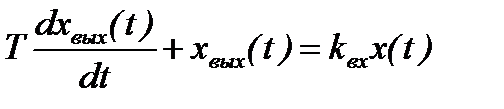, (2.43)

где k, T – коэффициент усиления и постоянная времени звена соответственно.

Операторное уравнение звена:

,

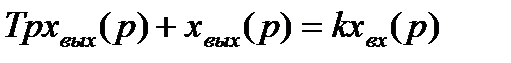а передаточная функция

.

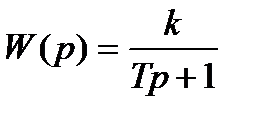Пример технической реализации апериодического звена первого порядка – RС-цепочка, поскольку напряжение, приложенное к ней (входной сигнал), и протекающий в цепи ток (выходной сигнал), связаны между собой уравнением Кирхгофа вида (2.43).

Амплитудно-фазовая характеристика звена имеет вид:

= = .

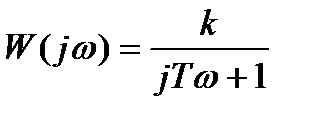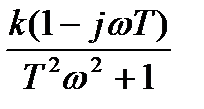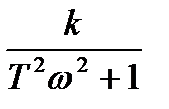
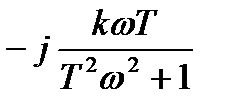Вещественная и мнимая частотные характеристики:

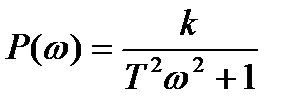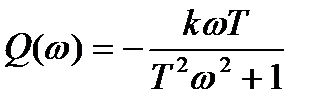; . (2.44)

Складывая выражения (2.44), получим:

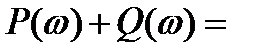
. (2.45)

Рис. 2.12. АФХ апериодического звена первого порядка

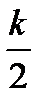
k

Возведя обе части выражения (2.45) в квадрат и прибавляя к обеим частям полученного равенства слагаемое (k/2)², получим:

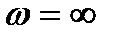
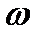
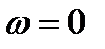
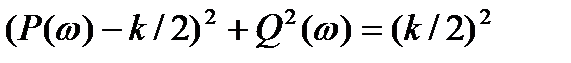. (2.46)

Из (2.44) – (2.46) следует, что АФХ звена имеет вид расположенной в четвертом квадранте полуокружности (рис. 2.12) с радиусом k/2 , центр которой находится на действительной положительной полуоси в точке с координатами (k/2; 0).

В соответствии с формулой разложения (2.15) переходная функция звена имеет вид:

h(t) = .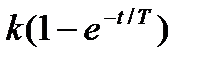

Функция веса может быть найдена по фор­муле (2.23):

w(t) = .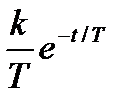

Графики временных характеристик звена приведены на рис. 2.13.

Амплитудно- и фазо-частотная характеристики звена:

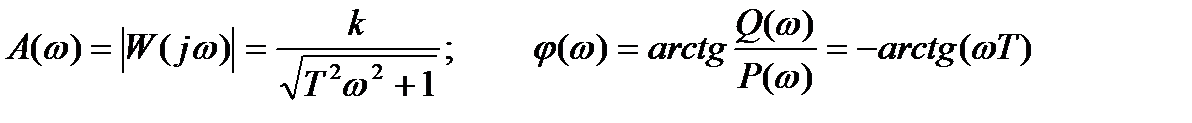. (2.47)

Логарифмическая амплитудно-частотная характеристика звена

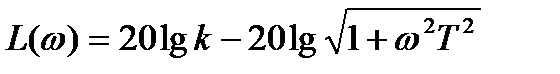. (2.48)

Предварительно построим приближенную характеристику L(ω) в низкочастотном диапазоне до частоты сопряжения 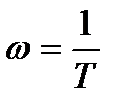, пренебрегая в выражении (2.48) слагаемым, зависящим от частоты, так как оно много меньше единицы. В результате, получим:

.

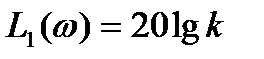На графике (рис. 2.14) этому выражению соответствует прямая линия, параллельная оси частот. На частотах, много больших частоты сопряжения 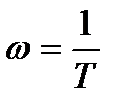, пренебрежем единицей. Тогда формула (2.48) приобретает вид:

.

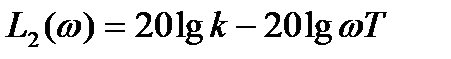Так как частота по оси абсцисс откладывается в логарифмическом масштабе, то этому выражению соответствует прямая линия с наклоном -20 дБ/дек.

Рис. 2.13. Переходная функция и функция веса апериодического звена первого порядка

-20 дБ/дек

1/Т

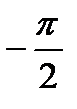
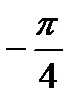
3 дБ

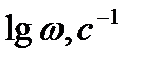
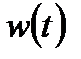
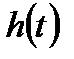
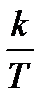
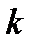
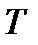
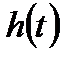
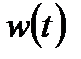
Рис. 2.14. Логарифмические амплитудно- и фазо-частотная характеристики апериодического звена

Характеристику, составленную из прямолинейных от­резков 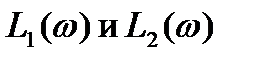, называют асимптотической. Наи­большее отклонение асимптотической характеристики от точной получается на частоте сопряжения 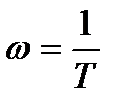: оно равно -3 дБ.