Дифференцирующее звено

Подставив в уравнение (1.63) значения b₁ = 0 и a₀ = a₁ = 0, получим уравнение состояния следующего вида:

a₂ y(t) = b₀ x′(t) (1.81.)

Уравнение идеального дифференцирующего звена будет иметь следующий вид:

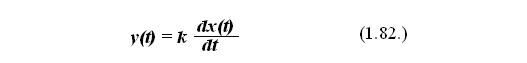
В данном случае k – передаточный коэффициент звена, размерность которого определяется отношением размерности выходного параметра к скорости изменения величины входного параметра.

Передаточная функция идеального дифференцирующего звена может быть найдена с помощью преобразования по Лапласу и будет иметь вид:

W(p) = kp (1.83.)

Переходная функция идеального дифференцирующего звена будет выражена:

h(t) = k δ(t) (1.84.)

Вышеуказанные функции являются нереализуемыми физически, потому что могут иметь бесконечные значения.

На практике обычно применяют последовательное соединение дифференцирующего и апериодического звеньев, т.к. инерционное звено ограничивает усиление на высоких частотах и в диапазоне рабочих частот характеристики получившегося звена близки к требуемым.

Для получения АФЧХ идеального дифференцирующего звена подставим в выражение (1.83.) jwвместо р, и получим:

W(jω) = jkω(1.85.)

основании данного выражения определим АЧХ идеального дифференцирующего звена:

A(ω) = kω(1.86.)

и ФЧХ идеального дифференцирующего звена:

j(w ) = arctg(¥) = π/2 (1.87.)

Графическое представление частотных характеристик идеального дифференцирующего звена изображено на рисунке 34.

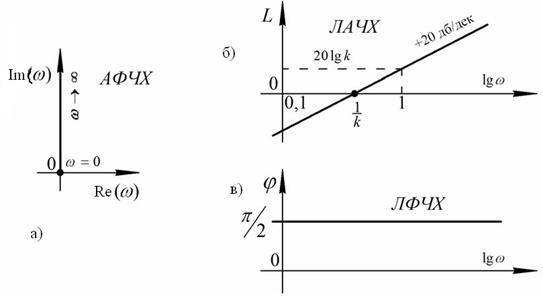
Рис.34. Графическое представление частотных характеристик идеального

дифференцирующего звена

Анализируя графики можно увидеть, что амплитуда выходных колебаний постоянно растет с ростом частоты входных колебаний. Сдвиг по фазе является постоянным, значение его равно π/2.

W(p) = kp /(Tp+1) (1.88.)

Временные характеристики дифференцирующего звена с замедлением и его реальное представление изображено на рисунке 35.

При входной частоте колебанийω ® ¥ передаточный коэффициент звена стремится к k/T. Сдвиги по фазе между входными и выходными параметрами колебаний принимают наибольшее значение при низких частотах.

При высокой частоте входных колебаний сдвиг по фазе стремится к нулю.

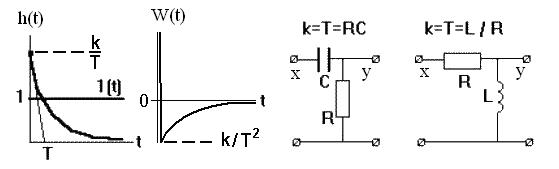
Рис.35 Временные характеристики и варианты реального представления

дифференцирующего звена с замедлением