Составление и линеаризация дифференциальных уравнений САУ

Процессы, происходящие в САУ, в общем случае описываются нелинейными дифференциальными уравнениями, которые могут быть решены лишь в отдельных редких случаях. Однако для достаточно большого числа систем эти уравнения с приемлемой для решения практических задач точностью могут быть заменены линеаризованными.

Рассмотрим принцип линеаризации на примере системы, у которой входной 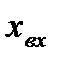и выходной 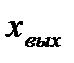сигналы связаны нелинейной статической зависимостью 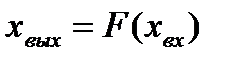. Пусть в установившемся режиме величина входного сигнала равна 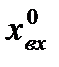и его отклонения от этого значения в переходных процессах достаточно малы.

Разложив нелинейную зависимость 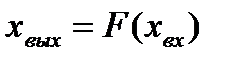в ряд Тейлора в окружности точки установившегося режима и, отбросив члены ряда выше первого порядка малости, получим следующую приближенную зависимость:

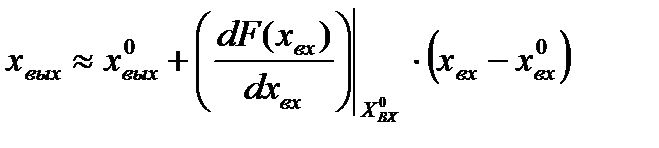, (2.1)

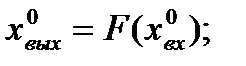
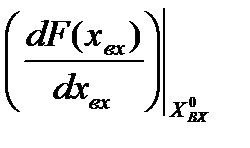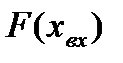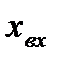где - значение производной функции по при подстановке в выражение этой производной значения = .

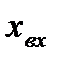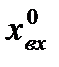Рис. 2.1. Линеаризация статической нелинейности

Выражение (2.1) можно переписать в виде:

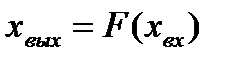
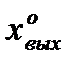
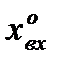
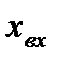
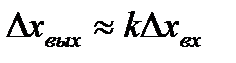, (2.2)

где ; ;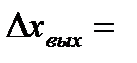

.

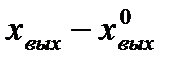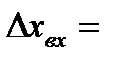
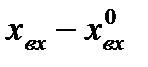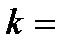
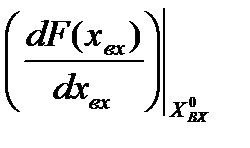Проведенная линеаризация имеет простую графическую интерпретацию: она соответствует (рис. 2.1) замене действительной нелинейной характеристики касательной к ней в точке, соответствующей установившемуся режиму. Коэффициент k в выражении (2.2) равен тангенсу угла наклона этой касательной относительно оси 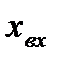. Поэтому его величина может быть найдена простым графическим построением без нахождения аналитического выражения нелинейной зависимости 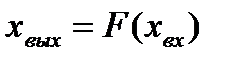и ее производной.

В более общем случае, система описывается нелинейным дифференциальным уравнением, связывающим производные по времени входного и выходного сигналов:

.

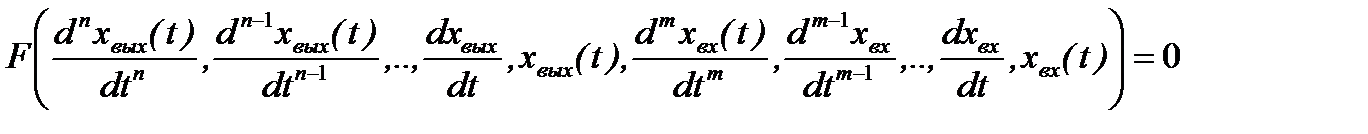(2.3)

Разложив нелинейную функцию (2.3) в ряд Тейлора в точке установившегося движения, получим следующее линейное дифференциальное уравнение для приращения переменных:

….+ …

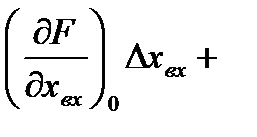
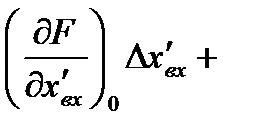
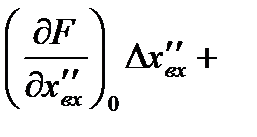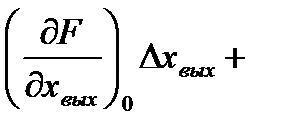
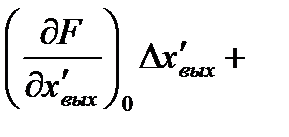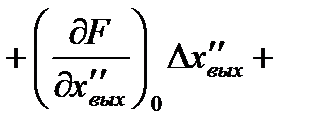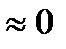+…… ….. , (2.4)

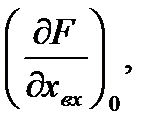
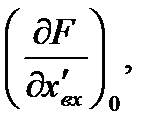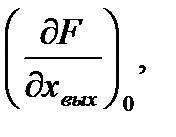
где .., 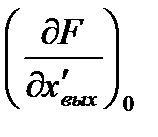и т.д. – значения производных функции (2.3) полученные при подстановке значений входного и выходного сигналов, соответствующих установившемуся режиму.

Следовательно, процедура линеаризации нелинейных систем дает возможность описать их линейными дифференциальными уравнениями в отклонениях. Очевидно, что допустимость такой линеаризации ограничена требованием к незначительности отклонений сигналов от их установившихся значений. Кроме того, поскольку такая линеаризация основана на разложении в ряд Тейлора, она применима только к непрерывно дифференцируемым нелинейностям.

Нелинейные звенья и системы, не удовлетворяющие этому требованию, называются существенно нелинейными. К существенно нелинейным звеньям относятся звенья с прерывистыми характеристиками, например, звенья с релейными характеристиками или неоднозначными характеристиками типа петли гистерезиса.