Анализ уравнений двухгироскопного компаса

Для определения характера движения главной оси гиросферы разрешим систему уравнений (2.7) относительно каждой ее переменной. Для этого запишем упомянутую систему в символической форме, принимая 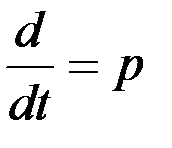. В результате найдем:

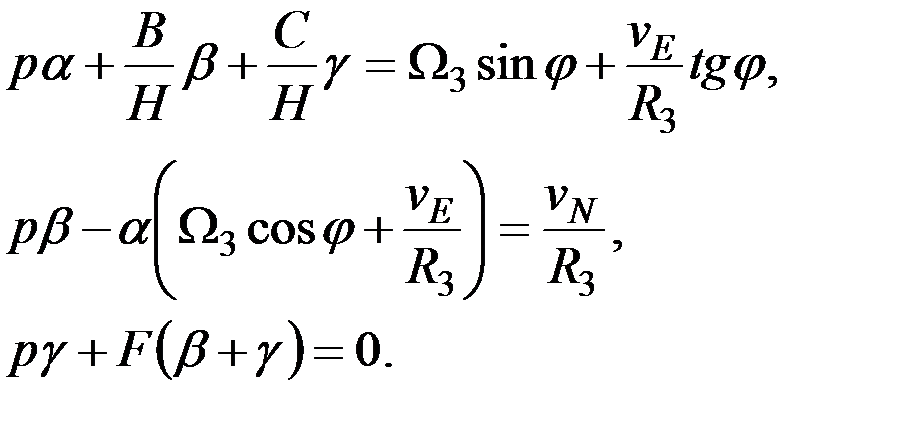(2.8)

Решения этой системы определяются формулами Крамера:

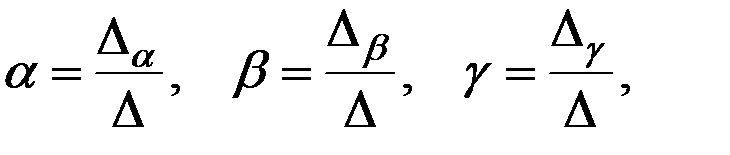(2.9)
где Δ – характеристический определитель, составленный из коэффициентов левой части системы (2.8); Δ_α, Δ_β и Δ _γ – частные определители, полученные путем замены коэффициентов при рассматриваемой переменной правыми частями уравнений (2.8).

(2.10)

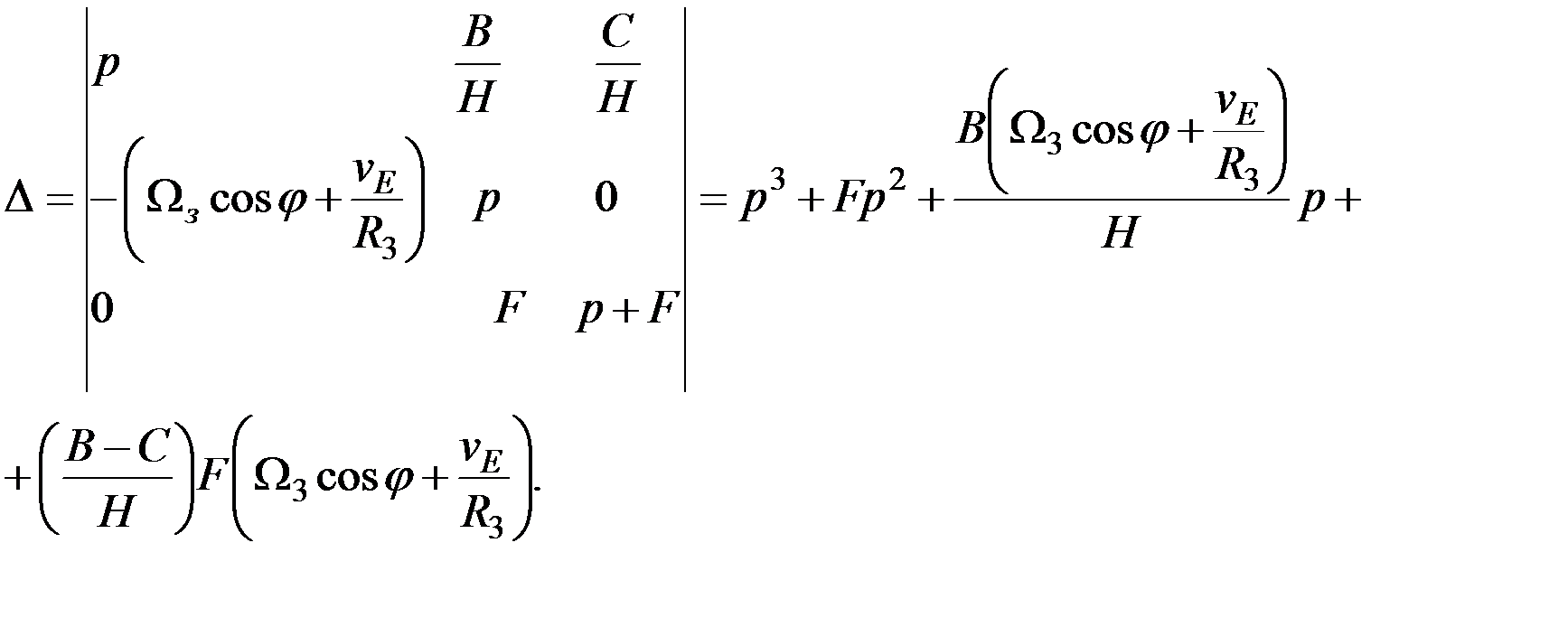
(2.11)

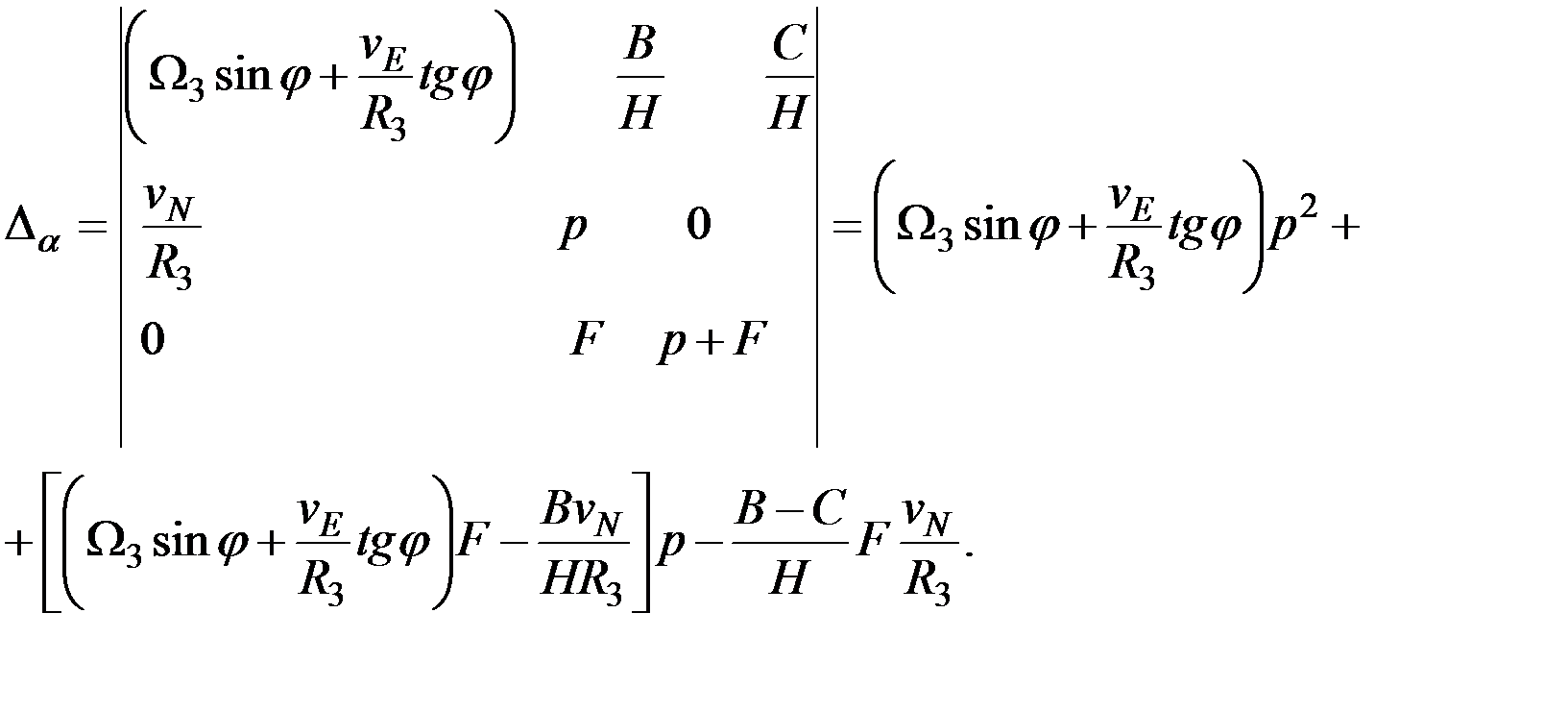
Вычисляя аналогично остальные частные определители, найдем:

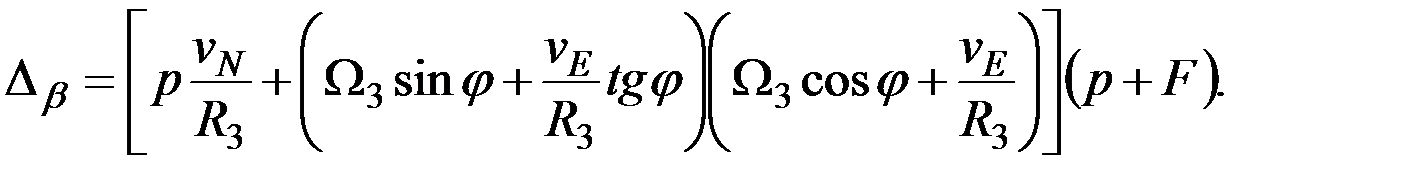(2.12)

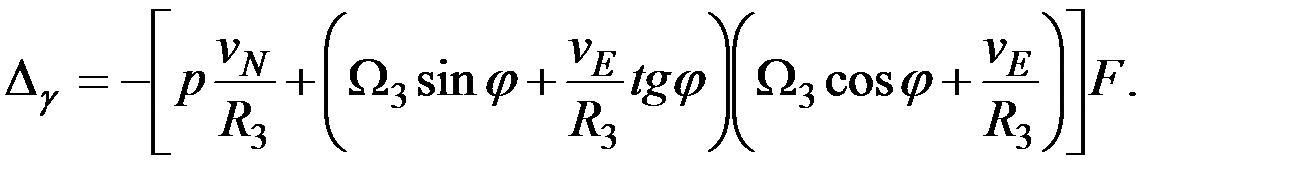(2.13)

Подставляя полученные значения определителей в равенства (2.9) и учитывая, что

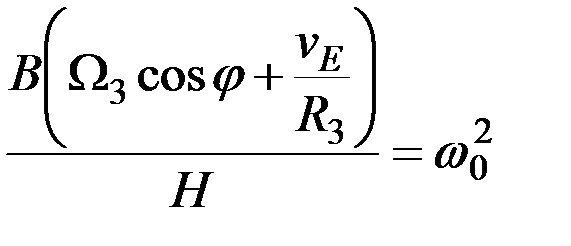, (2.14)

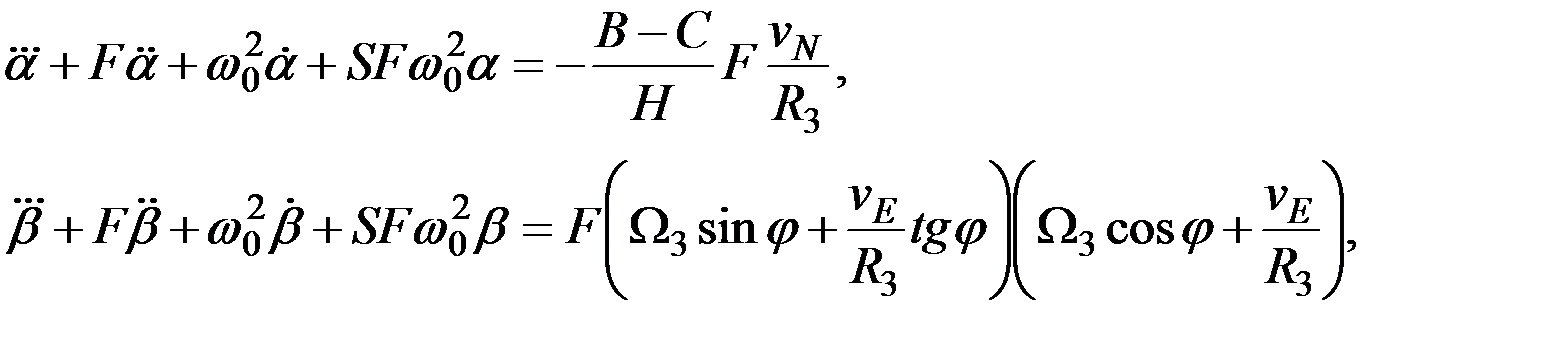
где 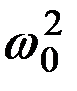- частота собственных незатухающих колебаний гиросферы, работающей на подвижном судне, а также принимая во внимание равенства 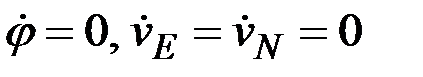, найдем:

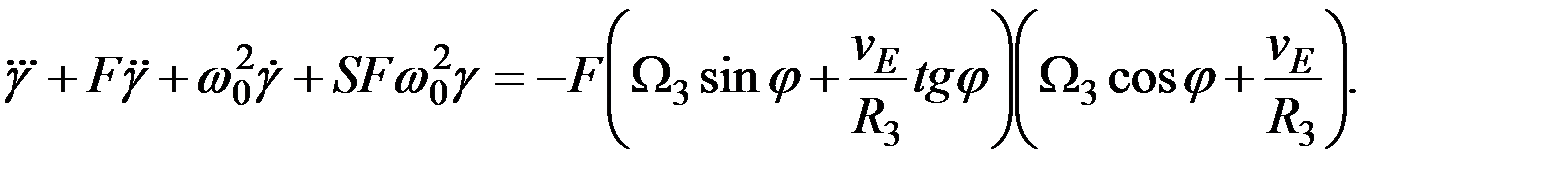
(2.15)

Здесь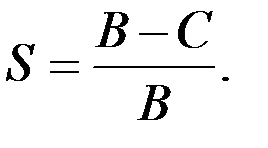

Решение уравнений (2.15) складывается из общих решений соответствующих им однородных уравнений и частных решений полных уравнений. Характер общего решения для всех трех уравнений одинаков, так как одинаковы структуры их левых частей. Поэтому достаточно исследовать собственное движение только по одной переменной, например, по углу α. Однородное уравнение, соответствующее первому уравнению (2.15) имеет вид:

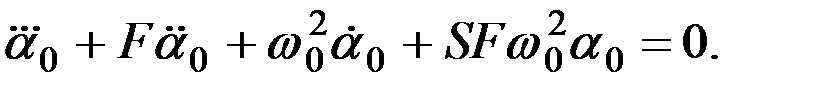(2.16)

Ему соответствует характеристическое уравнение

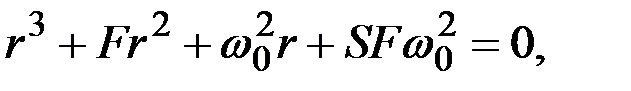(2.17)

которое имеет три корня. Параметры гироскопов подбирают таким образом, чтобы один из указанных корней был вещественным и отрицательным, а два других - комплексными с отрицательными вещественными частями:

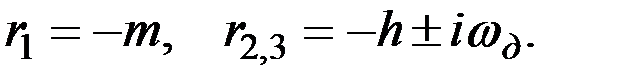(2.18)

Решение уравнения (2.16), соответствующее данным корням, может быть записано в следующем виде:

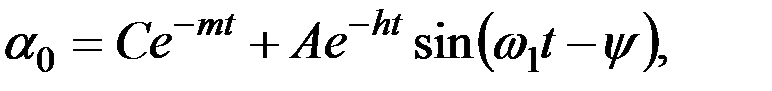(2.19)

где С и А – произвольные постоянные, зависящие от начальных условий.

Равенство (2.19) показывает, что собственное движение оси гиросферы складывается из двух составляющих: экспоненциального, определяемого первым слагаемым, и гармонического, с амплитудой, убывающей во времени (рис. 2.10). Как правило, экспоненциальная составляющая переходного процесса затухает быстрее гармонической. Так, в гирокомпасе “Курс” она перестает оказывать ощутимое влияние на общую кривую переходного процесса спустя 60 – 80 минут после его начала, в то время как общая продолжительность колебаний оси гиросферы может достигать шести часов. Указанное обстоятельство позволяет выделить две части переходного процесса: непериодическую, когда влияние первого слагаемого равенства (2.19) ощутимо, и периодическую, когда этим влиянием можно пренебречь. Такое деление в ряде случаев является весьма полезным.

Рассматриваемая кривая имеет не только познавательное значение. Она может быть использована для диагностики технического состояния изделия. В эксплуатационной документации на прибор, как правило, указываются количественные значения параметров переходного процесса. Чаще всего его характеризуют величиной периода затухающих колебаний гиросферы и фактором затухания. Соответствие указанных параметров, полученных в результате обработки переходного процесса, их значениям, приведенным в документации на прибор, является необходимым, но недостаточным условием, свидетельствующем о пригодности компаса к эксплуатации.

Практически кривую переходного процесса можно снять с курсограммы, записанной на отрезке времени от момента включения ГК до момента установления гиросферы в меридиан, или построить ее, используя показания, репитера. В процессе анализа непериодическую часть кривой и ее концевую часть, на которой колебания гиросферы плохо различимы, отбрасывают. Используя периодическую часть снимают значения 0,5Т₁, 0,5Т₂, и т.д. полупериодов затухающих колебаний и вычисляют среднее значение периода:

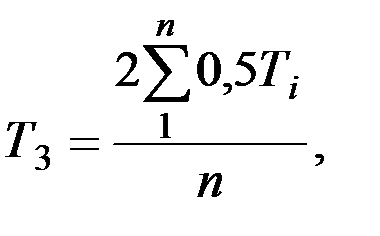(2.20)

где п – количество измеренных полупериодов.

После этого снимают значения амплитуд А₁, А₂, … и вычисляют среднее значение фактора затухания

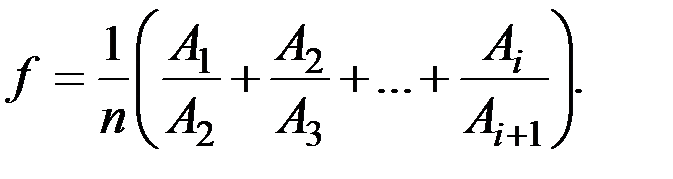(2.21)

Здесь п – количество слагаемых в скобках равенства (2.21).

Зная фактор затухания можно определить параметр h, входящий выражение (2.19):

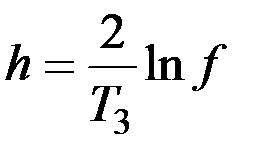(2.22)

и при необходимости пользоваться им.

Перейдем к определению установившегося положения оси гирокомпаса, которое она займет поле прекращения переходного процесса. В этом положении все производные, характеризующие изменение исследуемых параметров, будут равны нулю. Поэтому из уравнений (2.15) найдем:

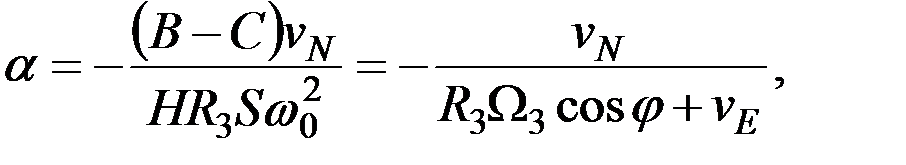
(2.23)

Полученные частные решения показывают, что ни один из интересующих нас параметров не имеет нулевое значение. Установившееся значение угла α отклонения гиросферы от плоскости истинного меридиана соответствует скоростной девиации гироскопического компаса, которая, как это указывалось выше, является методической ошибкой прибора, и, если она специально не скомпенсирована, существует в любых моделях гирокомпаса.

Частное решение по углу β отклонения гиросферы от плоскости горизонта имеет тот же физический смысл, что и для недемпфированного компаса. Разница заключается в том, что гидравлический успокоитель колебаний гиросферы несколько ослабляет влияние смешения центра масс самой гиросферы, поэтому для обеспечения требуемой ее азимутальной прецессии необходимо большее отклонение оси от плоскости горизонта, что и имеет место в силу уменьшения величины знаменателя выражения для угла β.

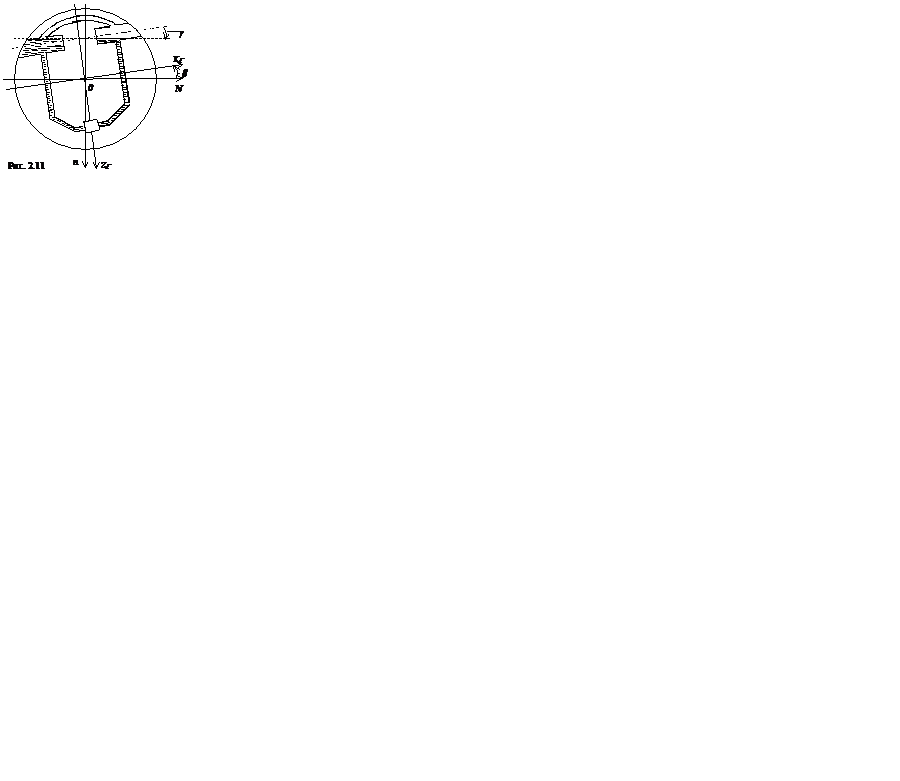
Вполне очевидно, что ввиду наличия отклонения главной оси гиросферы от плоскости горизонта уровень жидкости в сосудах успокоителя будет не одинаков. Поскольку мениски жидкости в сосудах лежат в плоскости горизонта (рис. 2.11) то угол γ, определяющий их положение, будет равен углу β, взятому с обратным знаком.

Важно!

Наиболее существенной из указанных погрешностей для решения вопросов навигации является скоростная девиация. Она непосредственно влияет на точность определения курса судна и поэтому в процессе плавания должна учитываться или быть скомпенсированной теми или иными способами. Выше было указано, что существуют два способа коррекции скоростной девиации: путем приведения чувствительного элемента гирокомпаса в истинный меридиан и путем введения поправок в устройства индикации курса и сигналы, направляемые различным потребителям данной информации. В связи с тем, что рассматриваемые ГК имеют автономный чувствительный элемент, исключается возможность его приведения в истинный меридиан, поэтому главная ось двухгироскопной гиросферы всегда находится в плоскости компасного меридиана.

Простейшие базовые модели ГК могут не иметь устройств коррекции скоростной девиации. В этом случае необходимо вносить поправку по данным специальных таблиц. Однако большинство этих моделей комплектуются корректирующими устройствами по просьбе заказчика. Современные системы коррекции ГК наряду со скоростной девиацией устраняют и другие существенные с практической точки зрения его ошибки.

В силу автономности чувствительного элемента ГК отклонение гиросферы от плоскости горизонта также не корректируется.