Обобщенная структурная схема САУ

ОСНОВНые понятия и определения теории автоматического управления

1.1. Краткие сведения по истории развития систем автоматического управления

К числу определяющих моментов в истории развития систем автоматического управления обычно относят создание центробежного регулятора, запатентованного Дж. Уаттом в 1784 году, и предназначенного для регулирования скорости паровой машины. Регулирование осуществлялось двумя сбалансированными на одной оси грузами, вращающимися синхронно с валом машины и соединенными с дроссельной заслонкой, которая при центробежном перемещении грузов перекрывала проходное сечение парового патрубка. Установка паровой машины Дж.Уатта на транспортные объекты (повозки и корабли) привела к созданию паровозов и пароходов, что привело к появлению транспортного машиностроения.

Но очевидно, что потребность в использовании различного рода регуляторов возникла гораздо раньше – а именно при создании таких высокоточных механизмов, как часы. Сохранилось описание конструкции часов, которые Гюйгенс в 1657 году снабдил маятниковым регулятором хода. Гораздо более раннее упоминание об использовании автоматических устройств связано с именем Герона Александрийского, в работах которого рассматривается пневматическое устройство, предназначенное для автоматического открывания ворот храма, но которое так и не было реализовано практически. И лишь на рубеже XVIII и XIX столетий, в эпоху бурного развития промышленности в Европе началось широкое внедрение промышленных регуляторов. К первым автоматическими регуляторами этого периода, кроме упомянутого регулятора скорости Дж. Уатт, следует отнести автоматический поплавковый регулятор питания котла паровой машины, внедренный в 1765 году И.И. Ползуновым, то есть почти на двадцать лет раньше регулятора Уатта, а также система программного управления ткацким станком, разработанная Жаккаром в 1804-1808 годах. В этот же период начинает развиваться и теория автоматического управления, формируется ряд важных принципов автоматики: принцип регулирования по отклонению Ползунова-Уатта и принцип регулирования по возмущению Понселе. Первые публикации по исследованию регуляторов появляются в двадцатых–тридцатых годах XIX века. Д.С. Чижов опубликовал один из первых трудов в 1823 году. Значительный вклад в теорию внесли три фундаментальные работы, содержащие по существу изложение основ новой науки: Д.К. Максвелла «О регуляторах» (1866 г.) и две работы И.А. Вышнеградского «Об общей теории регуляторов» (1876 г.) и «О регуляторах прямого действия» (1877 г.). Их публикация позволило дать общий подход к исследованию разнообразных по своей физической природе систем, заложить основы теории устойчивости и установить ряд важных общих закономерностей регулирования по принципу обратной связи. Начинается усиленная разработка математического аппарата, в частности были разработаны алгоритм для определения устойчивости систем по виду корней характеристического уравнения и критерии устойчивости систем Раусcа (1877 год) и Гурвица (1895 год). В 1892 г. выходит в свет работа А.М. Ляпунова "Общая задача об устойчивости движения", окончательно сформулировавшая теорию регулирования как особую область знаний, опирающуюся на строго доказанный математический аппарат и конкретные практические приложения.

Важное место в теории регулирования занимают работы Н.Е. Жуковского «О прочности хода» и «Теория регулирования хода машин» (1909 г.).

В период с 1900 по 1940 гг. появляется целый ряд работ, рассматривающих приложения теории регулирования к разнообразным техническим процессам. Особенно чётко мысль о теории регулирования как о дисциплине общетехнического характера проводится в ряде работ И.И. Вознесенского (период с 1922 по 1942 гг.), руководителя одной из крупнейших научных школ в этой области.

Быстрое развитие систем автоматического управления вело к необходимости создания более эффективных методов исследования. Появляются работы Найквиста (1932 г.) и Михайлова (1938 г.), касающиеся теории устойчивости. Частотные критерии устойчивости, разработанные А.В. Михайловым, быстро вошли в практику. В 1946 г. Т Броде и Я. Маккол ввели в рассмотрение логарифмические характеристики.

В эти же годы усилия исследователей направляются на разработку общих основ теории нелинейных систем. Одно из важнейших направлений, исследование устойчивости нелинейных систем, основывающееся на работах А.М. Ляпунова (1896 г.), развивалось в работах Н.Г. Четаева (1945 г.), А.И. Лурье (1944–1951), А.М. Летова и др.

В трудах Г.В. Щипанова, В.С. Кулебякина, Б.Н. Петрова и других были разработаны теория автоматического регулирования по возмущению и теория компенсации возмущений.

В.В. Казаничевым, А.П. Юркевичем, А.А. Фелдбаумом, А.А. Красовским и другими были сформулированы и исследованы принципы экстремального управления и разработана теория экстремальных систем, а также созданы основы теории оптимального управления.

В настоящее время повышение значимости теории автоматического управления обусловлено еще и тем, что принципы управления, определяющие функционирование технических объектов, во многом аналогичны тем законам, по которым развиваются биологические, экономические и социальные системы. Это обуславливает возможность формирования обобщенной теории управления, подтверждающей слова французского ученого Блеза Паскаля: «Не следует себя обманывать: мы являемся в такой же степени автоматами, в какой и мыслящими существами…»

Обобщенная структурная схема САУ

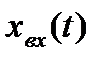
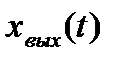
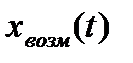
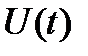
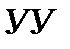
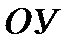
Рис. 1.1. Обобщенная структурная схема САУ

Система автоматического управления (рис 1.1) содержит: устройство управления(УУ) или регулятор, на вход которого подается задающее воздействие(входной сигналили совокупность сигналов) х_вх(t). Задающее воздействие определяет требуемый закон управления. В результате этого воздействия на выходе регулятора вырабатывает управляющее воздействие U(t), которое поступает на вход объекта управления (ОУ).

Под ОУ в данном курсе понимается любое техническое устройство (станок, самолет, турбина и т.д.), для функционирования которого необходимы специально организованные воздействия U(t). Качество управления оценивается по значению выходной величиныобъекта х_вых(t) – это обычно главный технологический параметр (скорость, мощность, производительность и т.д.).

Наряду с х_вх(t), внешним по отношению к рассматриваемой САУ явяляются возмущающее воздействие х_возм(t), которое, как и U(t), приложено к ОУ. К числу таких возмущений можно отнести момент сопротивления при металлообработке, колебание напряжения в сети, ветровую нагрузку и т.д. Возмущающие воздействия искажают требуемый закон управления. Очевидно, что в первом приближении задача синтеза САУ состоит в разработке такого УУ, с которым и при наличии существенных возмущающих воздействий отклонение требуемого закона управления ОУ от фактического не превышает допустимых значений.

Классификация СAУ

Системы автоматического регулирования классифицируются по различным признакам.

1. По принципу построения, различают разомкнутые системы, системы с управлением по отклонению (с обратной связью) и системы с компенсацией возмущения.

В разомкнутых системах (см. рис. 1.1) управляющее воздействие U(t),

формируемое на выходе УУ, определяется только входным сигналом системы х_вх(t) и не зависит от выходной величины объекта регулирования х_вых(t). При наличии значительных возмущений или нестабильности параметров системы фактический закон изменения выходной величины может значительно отклоняться от заданного.

В соответствии с принципом управления по отклонению управляющее воздействие U(t) зависит от отклонения фактического закона изменения регулируемой величины от требуемого. Сигнал

х(t) = х_вх(t) - х_вых(t),

называемый ошибкой регулирования, формируется на элементе сравнения (ЭС). Информация о текущем значении регулируемой величины поступает в ЭС по каналу обратной связи (ОС). Наличие канала ОС делает структуру системы замкнутой (рис. 1.2.).

Рис. 1.2. Структура системы с управлением по отклонению

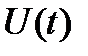
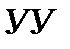
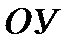
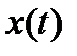
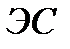
В общем случае ОС может быть не только отрицательной, но и положительной, при этом в ЭС входной и выходной сигналы системы складываются.

Рис. 1.3. Структура системы с компенсацией возмущения

В системах с компенсацией возмущения (рис. 1.3.) управляющее воздействие U(t) на выходе УУ зависит как от входного сигнала системы х_вх(t) , так и от возмущающего воздействия х_возм(t).

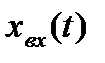
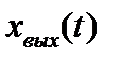
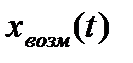
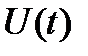
2. По виду входного сигнала САУ делятся на: системы стабилизации, входной сигнал которых является постоянной величиной (например, системы автоматической стабилизации скорости резания при металлообработке или системы стабилизации напряжения); системы программного управления, в которых входной сигнал является известной, заранее заданной функцией времени (например, система управления станков с ЧПУ); следящие системы, в которых входной сигнал заранее не определен и зачастую случаен (напри­мер, радиолокационные системы автоматического сопровождения цели).

3. Существенным при математическом описании систем является их деление на линейные и нелинейные. Для линейных систем выполняется принцип суперпозиции, суть которого заключается в следующем: если на вход системы поступает управляющее воздействие, которое можно представить в виде суммы k простых воздействий

,

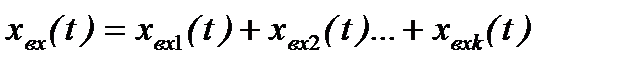то реакция системы (ее выходной сигнал) равна сумме реакций на каждое слагаемое х_вхi(t), 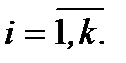При этом значение k и форма х_вхi(t) могут быть любыми.

Все реальные системы в технике и в природе, как правило, являются в большей или в меньшей степени нелинейными. Системы, нелинейность которых проявляется незначительно, можно, с приемлемой для практики точностью, описывать как линейные, используя более простые линеаризованные характеристики и уравнения. Очевидно, что для существенно нелинейных систем использование линеаризованных моделей недопустимо, и такие системы должны рассматриваться отдельно.

4. Различают стационарные и нестационарные САУ. Параметры стационарных систем неизменны, а у нестационарных параметры являются функциями времени или сигналов системы.

5. По виду зависимости регулируемой величины от внешнего воздействия различают статические и астатическиеСАУ. В последних, после завершения переходного процесса, вызванного внешним воздействием, значение регулируемой величины устанавливается равным заданному, т.е. в установившемся режиме ошибка регулирования равна нулю. В статических САУ регулируемая величина по окончании переходного процесса принимает значение, пропорциональное внешнему воздействию, при этом установившееся значение ошибки регулирования отлично от нуля.

6. Система относится к непрерывным, если все сигналы в ней являются непрерывными функциями времени. В дискретныхСАУ имеет место дискретный способ передачи и преобразования сигналов. Важнейшим классом дискретных систем являются цифровые системы, в структуру которых входят цифровые вычислительные устройства (контроллеры, микропроцессоры и т.п.).

7. В адаптивных САУ управляющее устройство позволяет обеспечить изменение алгоритмов управления и параметров системы (например, коэффициентов усиления звеньев), в результате чего достигается высокое качество работы системы.