Автомодельного ламинарного течения жидкости в трубе с использованием системы дифференциальных уравнений, описывающих течение жидкости в трубе
Уравнение (1.1) представляет частный случай более общего, соответствующего любому пространственному движению вязкой жидкости, закона линейной связи между тензором напряжений и тензором скоростей деформаций. Этот закон называется обобщенным законом Ньютона, а жидкости, удовлетворяющие этому закону, - ньютоновскими.
В соответствии с обобщенным законом Ньютона касательные напряжения tij пропорциональны относительным скоростям сдвиговой (угловой) деформации gij [2]:
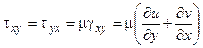
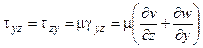 (1.10)
(1.10)
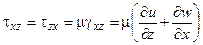
Нормальные напряжения представляются в виде суммы двух напряжений s и s¢:
sх = s + sх¢; sy = s + sy¢; sz = s + sz¢.
Напряжение s - среднее арифметическое трех нормальных напряжений sх, sу и sz: s = 1/3 (sх + sy + sz) = - р, а sх¢, sy¢ и sz¢ - добавочные нормальные напряжения, которые в соответствии с обобщенным законом Ньютона пропорциональны относительным скоростям линейной ei и объемной e деформации [2]:
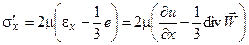
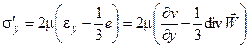
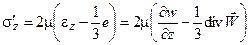
Т.е. в соответствии с обобщенным законом Ньютона нормальные напряжения записываются в виде:
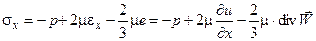
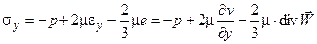 (1.11)
(1.11)
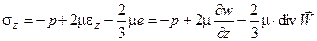
В формулах (1.10) и (1.11): tху, tух, tyz, tzу, tхz, tzx - касательные напряжения (первый индекс обозначает ось координат, нормальную к площадке, на которую оно действует, второй - ось, на которую оно проектируется); gху, gyz, gхz - скорости сдвиговых деформаций в плоскостях x0y, y0z и x0z; u, v и w - проекции вектора скорости 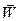 на оси координат x, y и z; sх, sу и sz - нормальные напряжения (индексы указывают оси координат, вдоль которых действуют эти напряжения); ex =
на оси координат x, y и z; sх, sу и sz - нормальные напряжения (индексы указывают оси координат, вдоль которых действуют эти напряжения); ex = 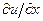 , ey =
, ey = 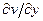 , ez =
, ez = 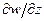 - скорости относительных линейных деформаций вдоль осей x, y и z; е =
- скорости относительных линейных деформаций вдоль осей x, y и z; е = 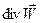 - скорость относительной объемной деформации (
- скорость относительной объемной деформации ( 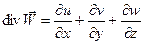 - дивергенция вектора скорости), р - давление.
- дивергенция вектора скорости), р - давление.
Величина m, являющаяся коэффициентом пропорциональности в формулах, связывающих касательные и добавочные нормальные напряжения со скоростями деформаций, называется динамическим коэффициентом вязкости.
Трехмерное установившееся (стационарное) изотермическое течение несжимаемой жидкости описывается уравнениями [2]:
- неразрывности
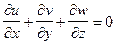 (1.12)
(1.12)
- движения
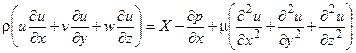
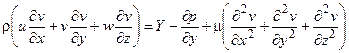 (1.13)
(1.13)
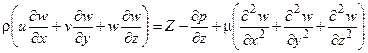
- состояния
r = const (1.14)
В уравнениях (1.12) - (1.14) X, Y, Z - проекции напряжения объемных сил на оси координат x, y и z.
Для решения системы уравнений (1.12)-(1.14) необходимо задать граничные условия: равенство нулю проекций вектора скорости на стенках трубы (гипотеза "прилипания"), распределение давления и проекций скорости во входном сечении трубы, распределение проекций вектора объемных сил X, Y и Z по объему трубы.
Используя уравнения (1.12) и (1.13), получим уравнения для несжимаемой жидкости, движущейся в цилиндрической трубе постоянного радиуса R. Будем считать, что труба является бесконечно длинной, а ось х совпадает с осью трубы. При течении в цилиндрической трубе v = 0 и w = 0 (v и w - проекции вектора скорости на оси y и z).
С учетом этого из уравнения неразрывности (1.12) для стационарного осесимметричного течения получаем
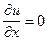 или u = u(y,z) , (1.15)
или u = u(y,z) , (1.15)
т.е. во всех сечениях трубы распределения скоростей одинаковы.
В случае установившегося течения несжимаемой жидкости при отсутствии объемных сил проекции уравнения движения (1.13) принимают вид:
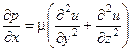 (1.16)
(1.16) 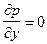 (1.17)
(1.17) 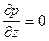 (1.18)
(1.18)
Из уравнений (1.16)-(1.18) следует, что давление р может быть только функцией х. Это означает, что в каждом сечении трубы давление постоянно и его изменение происходит при переходе от одного сечения к другому.
Так как правая часть уравнения (1.16) зависит только от y и z, а левая - только от х, то обе части должны быть равны одному и тому же числу:
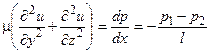 (1.19)
(1.19)
где (р1 - р2) - перепад давления на длине l трубы.
Интегрирование уравнения (1.19) удобнее проводить в цилиндрических координатах х = х, 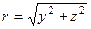 ,
, 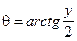 .
.
Учитывая, что
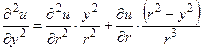 ,
, 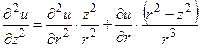
и заменяя частные производные полными в силу того, что u=u(r) и p=p(x), из (1.19) получим
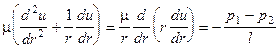 (1.20)
(1.20)
После интегрирования уравнения (1.20) имеем:
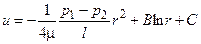 ,
,
где B и C - постоянные интегрирования.
Граничные условия (скорость конечна во всей области и равна нулю на стенках трубы) дают
B = 0; 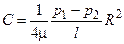
С учетом этого
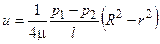 (1.21)
(1.21)
Уравнение (1.21) совпадает с уравнением (1.3), полученным ранее.
Выше было отмечено, что формула (1.1) является частным случаем формул (1.10). Действительно, при течении жидкости в трубе v = 0 и w = 0. Следовательно, c учетом симметрии течения согласно выражениям (1.10)
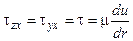
Дата добавления: 2017-03-12; просмотров: 2444;











