Алгоритмы нахождения корней уравнений.

Решение алгебраических уравнений численными методами состоит из двух этапов:

– отделение корней, т. е. отыскание достаточно малых интервалов
(a, b), в каждом из которых заключен один и только один корень;

– вычисление (уточнение) корня с заданной погрешностью.

Для отделения корней можно использовать алгоритм, схема которого приведена на рис. 5.9. На втором этапе используется один из известных алгоритмов уточнения значения корня. При этом любой из известных алгоритмов реализует вычисления в соответствии с итерационным циклом. Рассмотрим более подробно эти алгоритмы.

Метод итераций

Пусть задано уравнение f(x) = 0, имеющее один-единственный корень х на интервал (a, b), т. е. a ≤ x ≤ b.

Уравнение f(x) = 0 представим в виде, необходимом для реализации метода итерации x = φ(x).

Если в интервале (a, b) выполняется неравенство |φ'(x)| ≤ q < 1, то метод итерации применим к исходному уравнению, и приведет к уточнению корня с заданной точностью (процесс итерации сходится).

Приведение исходного уравнения f(x) = 0 к форме x = φ(x).может быть выполнено разными способами. Один из них сводится к следующему. Предположим, что 0 ≤ m ≤ f(x) ≤ M при a ≤ x ≤ b (если f(x) < 0, то достаточно уравнение f(x) = 0 умножить почленно на -1), тогда уравнение

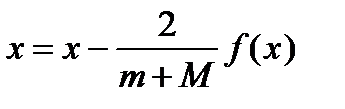
равносильно исходному уравнению f(x) = 0, имеет требуемую каноническую форму и

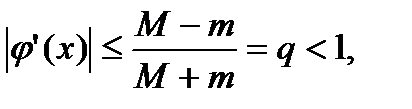
На рис. 5.11,а показан геометрический смысл первоначального уравнения f(x)=0. На этом рисунке точка х* является искомой. В результате тождественных преобразований исходного уравнения f(x)=0 к требуемому виду получаем геометрический смысл итерационного метода. На
рис. 5.11,б искомый корень х* определяет точку пересечения двух функций: у = х и у =φ(х).

Метод итерации состоит из последовательности следующих шагов: выбираем любое значение х = х₀ из интервала (a, b), вычисляем φ(х₀) и приравниваем его к новому значению корня x₁:

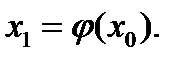
Далее этот процесс повторяется так, что k-я итерация состоит в вычислении

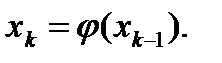
Погрешность ε_k на k-й итерации удовлетворяет неравенству

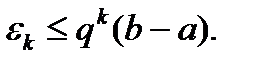
Процесс итерации проводим до тех пор, пока погрешность ε_k будет больше заданной погрешности ε. На рис. 5.11,б прямые со стрелками показывают итерационное движение вычислительного процесса к искомому значению х*.

В алгоритме метода итераций вычисляется последовательность значений

х₀, х₁, х₂, …, х_n, …

по формуле x_n = φ(x_n-1). Данная последовательность сходится к величине х*. Условие продолжения цикла

|x_n – x_n-1| > ε,

т.е. вспомогательная последовательность для контроля погрешности:

|x₁ – x₀|, |x₂ – x₁|, …, |x_n – x_n-1|, … .

Заметим, что в качестве вспомогательной можно использовать последовательность

|f(x₀)|, |f(x₁)|, |f(x₂)|, …, |f(x_n)| … ,

y

y= φ(x)

y=f(x)

y= x

а)

x0 x1 x2 x* x

y

x

которая сходится к нулевому значению.

Рис. 5.19. Алгоритм вычисления определенного интеграла по формуле Ньютона

0 a x* b x

Рис. 5.19. Алгоритм вычисления определенного интеграла по формуле Ньютона

Рис. 5.11. Геометрическая иллюстрация метода итераций

Рис. 5.19. Алгоритм вычисления определенного интеграла по формуле Ньютона

φ(x0)

φ(x1)

φ(x2)

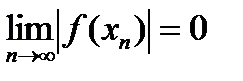
Поэтому условием продолжения цикла с предусловием может быть неравенство

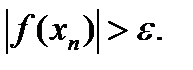
Пусть, например, необходимо найти с погрешностью ε = 10^-4 корень уравнения

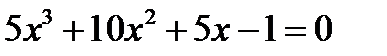
Приведем исходное уравнение к виду

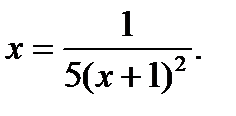
Для определения x₀ применим графический метод отделения корней, а именно построим график функций

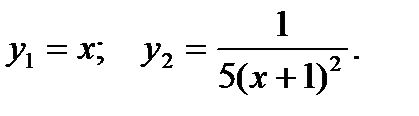
Нетрудно убедиться, что корень (точка пересечения этих графиков) принадлежит к отрезку [0, 1]. Поэтому

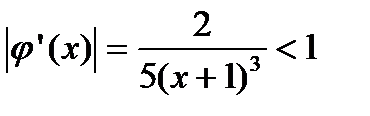
для всех 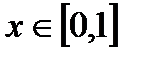метод итераций применим.