АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Итак, пусть требуется решить систему линейных алгебраических уравнений

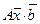(1)

Напомним, что в (1.1) A -квадратная матрица 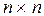с вещественными коэффициентами a_ij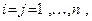 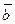- заданный вектор-столбец с вещественными компонентами, 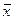- искомый вектор-столбец с n-компонентами.

Прежде чем применить какой-либо метод решения задачи (1) следует убедиться в том, что эта задача поставлена корректно. Будем говорить, что задача поставлена корректно, если:

а) решение задачи существует,

б) единственно,

в) непрерывно зависит от входных данных.

Как известно, для задачи (1) первые два требования в определении будут выполнены, если

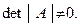
Третье же требование в (2) применительно к задаче (1) нуждается в некоторой детализации и связано с понятием обусловленности исходной матрицы A.

Методы решения СЛАУ (1) можно разделить на две группы: прямые и итерационные. В прямых методах нахождение решения задачи (1) осуществляется за конечное число действий. В итерационных методах определяется не само решение задачи (1) , а некоторая последовательность векторов 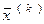(k- номер итерации) такая, что

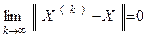(2)

К прямым методам решения определенных СЛАУ относятся: метод Крамера и метод Гаусса. Причем эти методы различаются по числу действий, необходимых для нахождения решения исходных СЛАУ. Мерой различия может служить число действий, необходимое для вычисления одного неизвестного. Ниже рассмотрим оба эти метода.

2.1. МЕТОД КРАМЕРА

Предположим, что в системе (1) у матрицы A размера 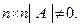Тогда матрица A имеет обратную A^-1, то есть A ×A^-1=A^-1 ×A=E. Умножим обе части выражения (1) слева на A^-1, получим

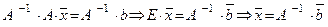(3)

Так как 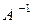= 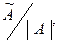то (3) можно записать так

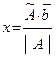(4)

где

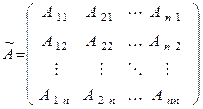а A_ij - алгебраические дополнения элементов, a_ij – определители матрицы A.

Расписывая выражение (4) покомпонентно, получим

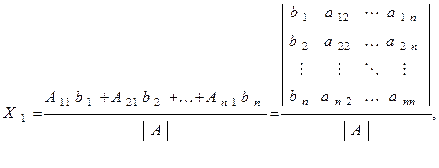
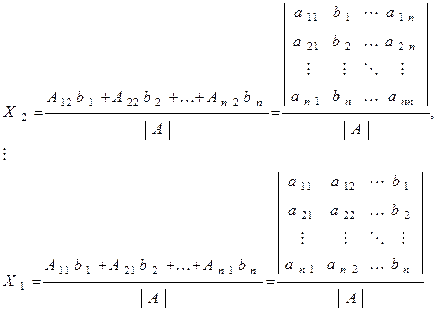
или

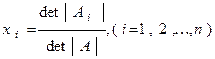(1.5)

где A_i - матрица, получаемая из A путем замены i-го столбца на столбец свободных членов. Формулы (5) называются формуламиКрамера.

ПРИМЕР. Решить по формулам Крамера систему линейных уравнений.

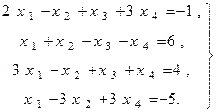
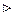Находим определител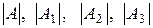и и 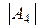, раскладывая их на миноры по элементам последней строки, а затем вычисляя по правилу треугольников. Имеем

,

,

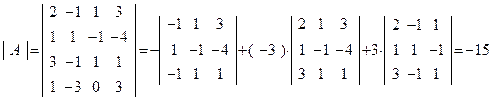
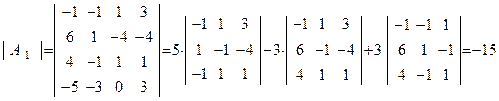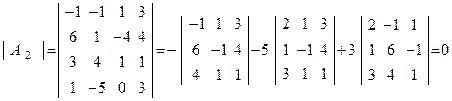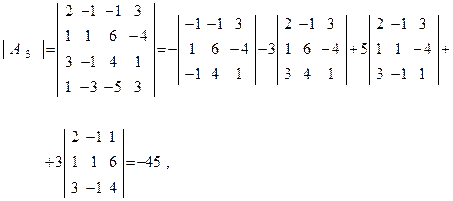
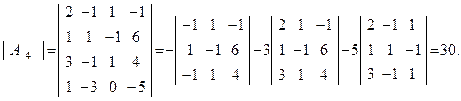
После определения значений определителе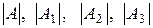й и 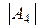по формуле Крамера находим решение системы:

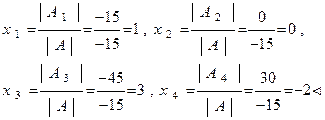
2.2. МЕТОД ИСКЛЮЧЕНИЯ ГАУССА

Пусть дана неоднородная СЛАУ, состоящая из n линейных уравнений с n неизвестными x₁ ,x₂ , ..., x_n и правыми частями b ,b₂ , ..., b_n:

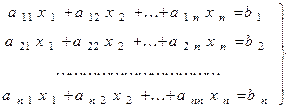. (1)

В матричной форме эта система может быть записана так:

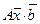(2)

где

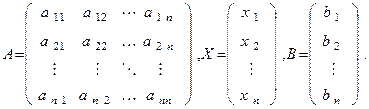
Ниже изложим метод для решения системы уравнений (1), основанный на последовательном исключении неизвестных. Этот метод связан с именем Гаусса. Имеет много различных вычислительных схем. Мы же приведем изложение, так называемой, схемы единственного деления.

Допустим, что коэффициент a₁₁¹0. Разделим коэффициенты первого из уравнений СЛАУ (1), включая и свободный член, на коэффициент a₁₁, который мы будем называть ведущим элементом 1-гошага, и обозначим

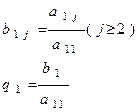. (3)

Получим новое уравнение, которое запишем так

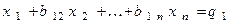(4)

Исключим теперь неизвестное 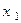из всех уравнений системы (1), начиная со второго, посредством вычитания из этих уравнений уравнения (3), умноженного соответственно на числа 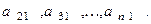Преобразованные уравнения будут иметь вид

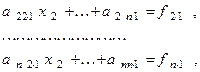(5)

где

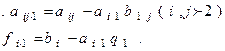(6)

Разделим далее коэффициенты первого из преобразованных уравнений на ведущий элемент 2-го шага 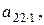который будем считать отличным от нуля. Мы получим уравнение

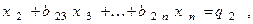
где

.

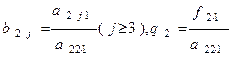Исключая неизвестное 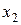из уравнений (5), начиная со второго, мы придем к уравнениям

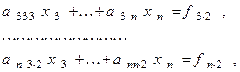
где

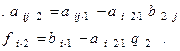
Продолжая процесс по той же схеме, на m-ом шагу мы получим уравнения

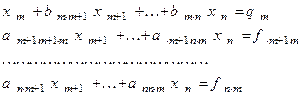(7)

где

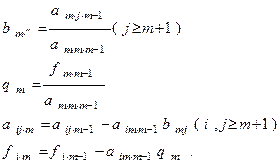
Итак, получаем

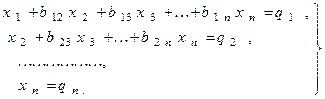(8)

или в матричной форме

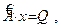(9)

где

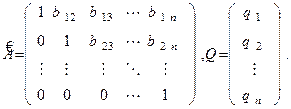
Отметим, что описанный процесс возможен только при условии неравенства нулю всех ведущих элементов 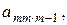так как по ходу процесса на них приходится производить деление.

Из системы (8) значения для неизвестных находим последовательно от x_n к x₁ по очевидным формулам

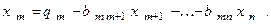
Итак, для решения данной системы по схеме единственного деления мы сначала строим вспомогательную треугольную систему, а затем решаем ее. Процесс нахождения коэффициентов треугольной системы мы будем называть прямым ходом, а процесс получения ее решения - обратным.

ПРИМЕР. Решить методом Гаусса систему уравнений

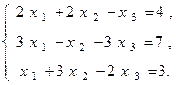
РЕШЕНИЕ.

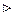Ш а г 1. Исключаем неизвестную x₁ из всех уравнений системы, начиная со второго. Для этого сначала разделим все члены его на коэффициент при x₁. Имеем

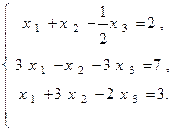(1)

Затем из второго уравнения системы (1) вычитаем первое, умноженное на 3

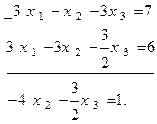
После этого из 3-го уравнения системы (1) вычтем первое

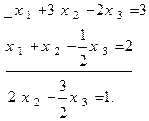
Теперь система уравнений примет вид

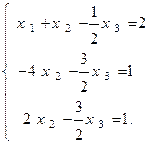(2)

Ш а г 2. Исключаем неизвестное x₂ из 3-го уравнения системы (2). Исключение выполняем с помощью 2-го уравнения системы (2), которое предварительно делим на коэффициент при x₂. После этого система запишется в виде

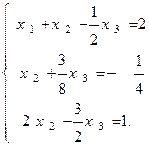
Затем вычитаем из третьего уравнения второе, умноженное на 2

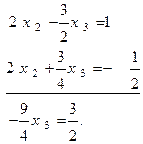
После этого исходная система (1) примет, так называемую, треугольную форму

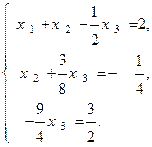(3)

Теперь легко найти значения неизвестных.

Ш а г 3. Определяем из третьего уравнения значение x₃

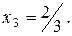
Ш а г 4. Подставляя значение x₂ во второе уравнение системы (3) находим

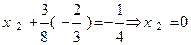
Ш а г 5. Значения x₃ и x₂ подставляем в первое уравнение и находим x₁

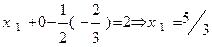
Итак

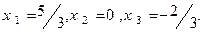
ЗАМЕЧАНИЕ.Метод Гаусса не требует предварительного анализа о совместимости системы.

а) Если система совместна и определена, то метод приводит к единственности решения.

б) Если система несовместна, то этот метод приводит к тому, что на каком-то шаге вместе с исключаемой неизвестной исключаются и все остальные неизвестные, а в правой части остается свободный член, отличный от нуля.

в) В методах типа Гаусса число действий Q(A), необходимых для нахождения решения задачи (1) имеет зависимость Q(A)=0·(n³). Если же матрица A диагональная, то Q(A)=n, а число действий q(A), необходимых для вычисления одного неизвестного в точности равно единице, то есть не зависит от n. Методы решения СЛАУ (1) называются экономичными, если q(A) не зависит или слабо зависит от n. Учеными показано, что для произвольной невырожденной матрицы существуют методы Q(A)=K·n^a, a=loq₂7. Однако, их логическая сложность и слишком большая величина константы K не дают этим методам практических преимуществ по сравнению с методами типа Гаусса. Поэтому можно считать, что для произвольной невырожденной матрицы A прямые методы с оценкой q(A)=0·(n²) являются оптимальными.

Дата добавления: 2016-06-05; просмотров: 1588;