Интерполирование функций.

1) Необходимость: приблизить f(x) более простой функцией ф(х), совпадающей в узлах x_i с f(x_i), если f(x) определена только в узловых точках (результат эксперимента) или очень сложно вычисляется.

Условия Лагранжа : ф(х, с₀, с₁…с_n) = f_i,

0 <_{_}i < n, где с_i - свободные параметры, определяемые из данной системы уравнений.

С помощью интерполяции решают широкий круг задач численного анализа: дифференцирование и интегрирование функций, нахождение нулей и экстремумов, решение дифференцированных и т. д. Термин интерполяция употребляют, если х заключено между узлами, если он выходит за крайний узел, говорят об экстраполяции(при которой трудно гарантировать надежность

приближения).

2) Пусть ф (х) = с₀ + с₁х + с₂х² +…+ с_nxⁿ (канонический вид полинома) ;сетка узлов может быть неравномерной.

Коэффициенты с_i определяются из условий Лагранжа:

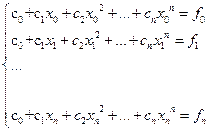Получившаяся СЛАУ относительно свободных

параметров с_i имеет решение, если среди узлов

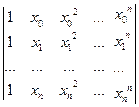х_i нет совпадающих.Ее определитель – определитель Вандермонда:

Общая блок-схема:

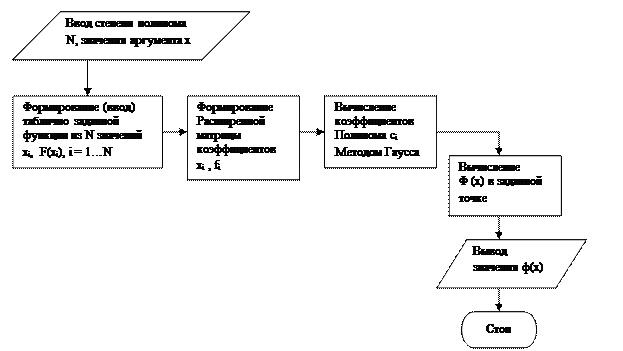
3) Пусть задано n+1 значение функции f(x) в узлах x_j

ф(х) = P_n(х) = 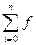_i 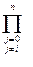(x-x_j)/(x_i-x_j) - полином Лагранжа.

Преимущества: потребуется решать СЛАУ для определения значения полинома в точке х.

Недостатки: для каждого х полином требуется читать заново.

Погрешность формулы: (*)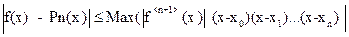

Увеличение числа узлов и, соответственно, степени полинома P_n(x) ведет к увеличению погрешности из-за роста производных .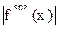

4) ф(х) = P_n(x) = A₀+A₁(x-x₀)+A₂(x-x₀)(x-x₁)+…+A_n(x-x₀)(x-x₁)…(x-x_n-1) - многочлен Ньютона для n+1 узла.

Коэффициенты Ф представляют собой разделенные разности и записываются в виде:

А₀ = f₀

A₁ = (f₀-f₁)/(x₀-x₁) = f₀₁

A₂ = (f₀₁-f₀₂)/(x₁-x₂) = f₀₁₂, где f₀₂ = (f₀-f₂)/(x₀-x₂)

A₃ = (f₀₁₂-f₀₁₃)/(x₂-x₃) = f₀₁₂₃ , где f₀₁₃ = (f₀₁-f₀₃)/(x₁-x₃) , а f₀₃ = (f₀-f₃)/(x₀-x₃)

и в общем случае A_k = (f_01…k-1-f_01…k)/(x_k-1-x_k)

Т.е. многочлен n-й степени выражается при помощи разделенных разностей через свои значения в узлах.

Преимущества: не решается СЛАУ, однако вычисление коэффициентов полинома не зависит от значения х и может быть вычислено только один раз. При добавлении нового узла также не происходит пересчета коэффициентов, кроме последнего.

После определения коэффициентов полинома Ньютона вычисление его значений при конкретных аргументах х наиболее экономично проводить по схеме Горнера:

P₂(x) = A₀+ (x-x₀)(A₁+(x-x₂)(A₃+…)…)

Погрешность определяется тем же соотношением (*)

Входящая в состав погрешности величина

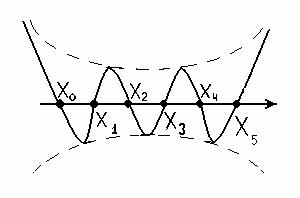
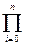(х-х_i) = w_n(x) ведет себя при постоянном шаге так, как показано на рисунке. Многочлен Ньютона имеет погрешность 0(hⁿ⁺¹) и обеспечивает n+1-й порядок точности интерполяции.

! Между разделенными разностями и производными соответствующих порядков существует соотношение f ^<n>(x) ~ n! F_01…n , где n – степень производной. Это используется в численном дифференцировании и при оценке погрешностей интерполяции.

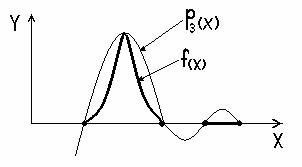! Можно строить полиномы, не только проходящие через заданные точки, но и имеющие в них заданные касательные (интерполяционный многочлен Эрмита) или заданную кривизну. Количество всех полагаемых условий должно быть n-1, если n – степень полинома.

Основной недостаток интерполирования с помощью многочленов – неустранимые колебания, которые претерпевает кривая в промежутках между узлами.

При этом повышение степени интерполяционного полинома для большинства решаемых уравнений приводит не к уменьшению, а к увеличению погрешности.