Вычисление описывающих функций.

1. Нелинейность кубического типа:

;

;

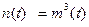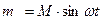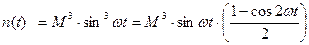
при этом учтем, что: ;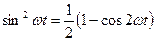

;

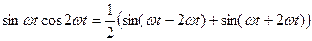
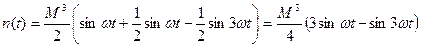Согласно допущению 3-й гармоникой пренебрегают , то

;

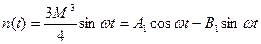Тогда ;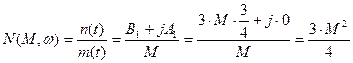

Эквивалентный коэффициент усиления нелинейности пропорционален квадрату амплитуды входного сигнала и поэтому сам по себе является нелинейным.

Идеальное реле.

Выходной сигнал идеального реле отражает факт появления сигнала на его входе.

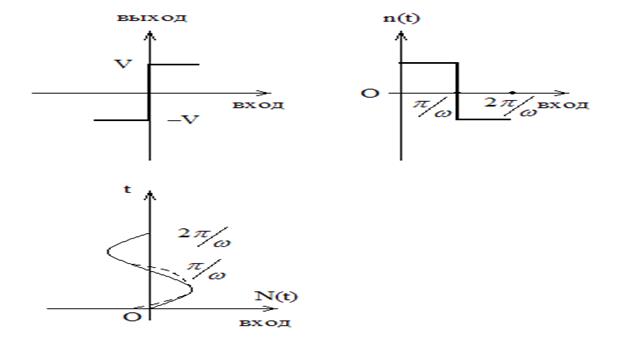
Поскольку выход является нечетной функцией, то 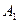=0 , поэтому:

;

;

;

;

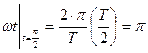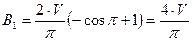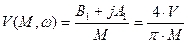Эквивалентный коэффициент обратнопропорционален амплитуде сигнала, но это очевидно, поскольку как не увеличивалась бы амплитуда на входе , на выходе она остается постоянной.

Таблица описывающих функций.

Описывающие функции для наиболее распространенных нелинейностей приведены в таблицах коэффициентов гармонической линеаризации. Для однозначных нелинейностей эти функции являются вещественными, т.к. они не приводят к появлению фазового сдвига синусоидального сигнала.

В случае неоднозначных нелинейностей прохождение через них синусоидального сигнала сопровождается фазовым сдвигом, поэтому для них описывающие функции, приводимые в таблицах являются комплексными.

Нелинейность N(M,w)

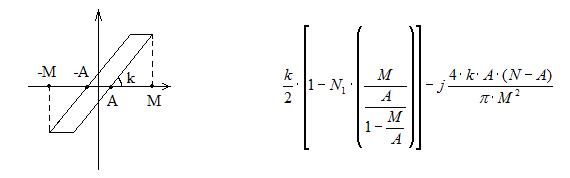
Для упрощения использования некоторых описывающих функций в указаных таблицах был выделен член 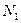, который является общим для многих из них. Табличные значения этого члена сведены в отдельную таблицу, часто приводят графики, номограммы.