Внешняя экспоненциальная функция процессового перехода. Зависимость кривизны участка перехода от масштабов функций.

Применим в качестве внешней функции экспоненту:

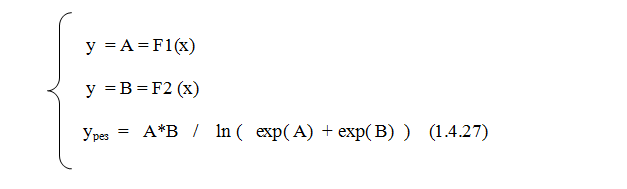
y_рез можно привести к виду:

y_рез = exp( ln(A) + ln(B) ) / ln ( exp( A) + exp( B) )

Кривизна участка перехода от одного процесса к другому у формулы «весов» с применением экспоненты сильно зависит от масштаба функции. Для примера на рис. 1.4.24. и рис. 1.4.25. приводятся графики функций разных масштабов. Для графика на рис. 1.4.24. функции заданы следующим условием:

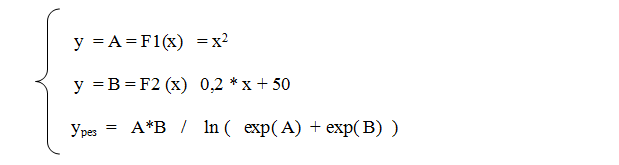
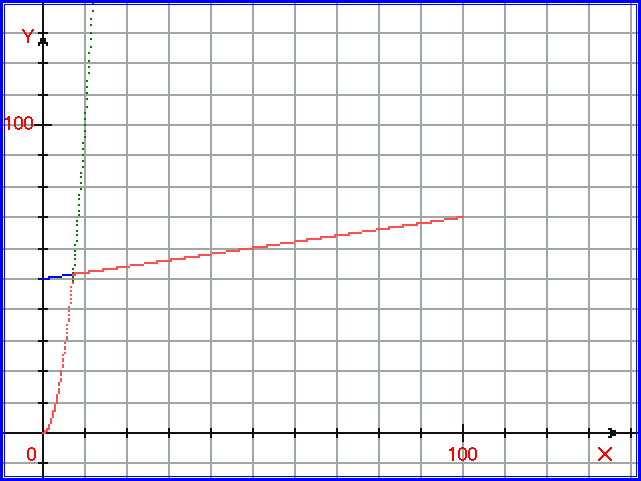
Рис. 1.4.24. График, иллюстрирующий одномерный процессовый переход. Зелёными точками построена функция y=A = x², синими точками построена функция y = B= 0,2*x+50, красными точками построена функция y_рез =A*B/ ln (exp(A)+exp(B)).

Для графика на рис. 1.4.25. функции заданы следующим условием:

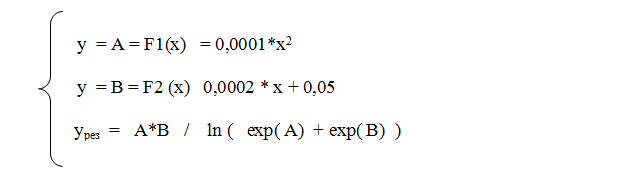
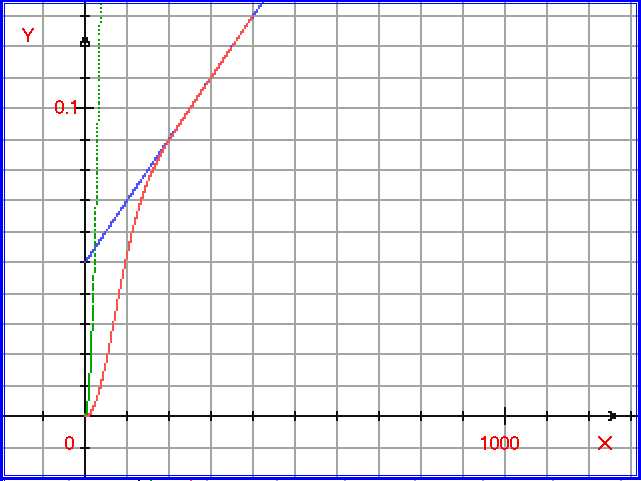
Рис. 1.4.25. График, иллюстрирующий одномерный процессовый переход. Зелёными точками построена функция y=A = 0,0001* x², синими точками построена функция y = B = 0,0002*x+0,05, красными точками построена функция y_рез = A*B/ ln (exp(A)+exp(B)).

Регулировать кривизну переходного участка удаётся, если несколько модифицировать формулу для y_рез , включив в её состав два коэффициента. Но такой метод пока не изучен, а результат сильно зависит от масштабов функций A и B. Для примера приведён вариант, представленный на рис. 1.4.26. Формула «весов» ассиметрична и применима не во всех случаях. Для графика на рис. 1.4.26. функции заданы следующим условием:

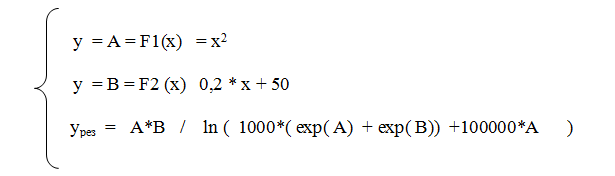
Рис. 1.4.26. График, иллюстрирующий одномерный процессовый переход. Зелёными точками построена функция y= A = x², синими точками построена функция y = B= 0,2*x+50, красными точками построена функция y_рез =A*B/ ln ( 1000*(exp(A)+exp(B)) +100000*A ).

Уравнение теперь имеет такой вид:

y_рез = A*B / ln ( К1*( exp( A) + exp( B)) +К2*A )

Коэффициенты К1 и К2 назовем коэффициентами, регулирующими кривизну участка перехода между процессами. Применив коэффициенты к формуле «весов» с внешней экспоненциальной функцией, зможно получить частичное моделирование участка «мини-макса» 1-й четверти. ( см. главу 1.4.3.7. ).

Для графика на рис. 1.4.27. функции заданы следующим условием:

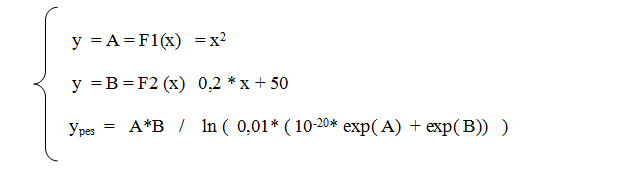
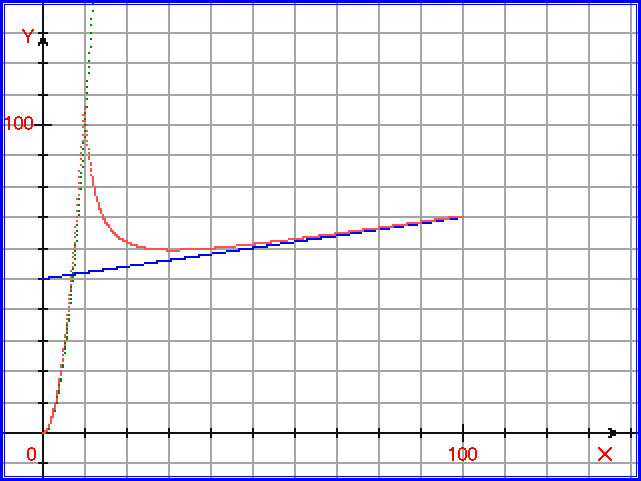
Рис. 1.4.27. График, иллюстрирующий одномерный процессовый переход. Зелёными точками построена функция y = A = x², синими точками построена функция y = B = 0,2*x+50, красными точками построена функция y_рез =A*B/ ln ( 0,01*(10-20* exp(A) + exp (B)) ).

Возможность частичного моделирования участка 1 ( см. рис. 1.4.17. ), которая продемонстрирована на рис. 1.4.27, также зависит от масштабов функций A и B.

Моделирование результирующей функции - двухмерного процессового перехода - для функции двух процессов. Двухмерный процессовый переход как существование двух процессов, ограничивающих рост друг друга (ООС). Понятие комплиментарности процессов.