Изображение электрических схем и условия их работы в виде аналитических функций.
Условия срабатывания устройств в РКС могут быть представлены в виде электрических схем с контактами.
На языке суждений а-л эти схемы можно представить структурной схемой:




 х у произведение контактов или суждений
х у произведение контактов или суждений
х







 сумма контактов или суждений
сумма контактов или суждений
у
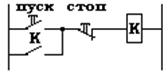
Если исполнительный элемент Х должен замкнуть контакты e1,у1,W1, то
 |  |  |
e1
у1 х1
W1
Это условие срабатывания может быть записано в символической форме
F(х1)= e1+ у1+ W1 , при помощи структурной формулы.
Структурная формула много элементной схемы составляется следующим образом:
записываются структурные формулы для цепей каждого исполнительного и промежуточного элементов.
F(х)=f1(a,b,c,…x,y,z…);
F(у)= f2(a,b,c,…x,y,z…);
…………………..
F( W) = fn(a,b,c,…x,y,z…).
Затем структурные формулы для элементов суммируются, производится упрощение преобразования на основании законов а-л и получают структурную формулу схемы.
F= f(a,b,c,…x,y,z…).
Синтез РКС производится в следующем порядке:
1. на основании требований, предъявляемых к электроустановкам, управление системой релейно-контакторной автоматики формируются
2. на основании условий работы СРКА определяется число и вид (характер) необходимых элементов;
3. составляется структурная формула для каждого элемента;
4. составляется структурная формула всей схемы СРКА; при составлении структурных формул нужно сделать все необходимые упрощения, пользуясь основными законами и соотношениями а-л, а так же понятиями о «0» и «1»:
х·1=х ; х+0=х;
х+1=1; х·0=0 .
Для обеспечения задачи составления структурных формул рекомендуется составлять таблицу включения по форме:
| Ситуация | Cитуация 1 | Ситуация 2 | ||||||||||
| такты | ||||||||||||
| состояние элементов схемы | А | +А | -А | |||||||||
| В | +В | |||||||||||
| С | +С |
«+» - вкл. ; «-» - выкл. ;
5. по структурной формуле строят структурную схему СРКА электроустановки;
6. по структурной схеме СРКА электрической установки строят ее принципиальную электрическую схему.
При модификации существующих схем рекомендуется их упрощать при помощи анализа. В этом случае, как и при синтезе схем, следует составлять структурные формулы всех элементов и путем преобразований получить оптимальную, структурную формулу СРКА электроустановки.
В процессе анализа удобно пользоваться так называемой формулой включения, которая описывает в символической форме последовательность работы схемы.
В таблице включений число строк в разделе состояний элементов равно числу элементов СРКА. Число столбцов в блоке равно числу первоначальных цепей СРКА, а число блоков (ситуаций) определяется количеством неповторяющихся совокупностей внешних условий.
Схемы автоматики могут быть комбинационные и последовательностные. Исполнительный элемент комбинационной схемы срабатывает при заданной комбинации входных сигналов. Последовательностные схемы содержат элементы памяти (триггеры, счетчики, регистры сдвига и реле с «само подхватом»).
В этих схемах исполнительный элемент срабатывает при заданной комбинации не только входных сигналов, но и элементов (сигналов), сработавших в результате появления определенных состояний исполнительных и промежуточных элементов схем.
Кроме того схемы могут быть асинхронными, срабатывающими в любой момент времени при появлении соответствующих комбинаций входных сигналов.
Схемы могут быть и синхронные (тактируемые), когда срабатывание происходит при условии одновременного формирования необходимой комбинации входных сигналов и синхронного импульса от тактового генератора.
В электроустановках релейно-контакторные схемы чаще всего относятся к асинхронным. Они могут быть и комбинационными и последовательностными, но процессы в этих схемах идут всегда параллельно.
Сети Петри.
Методом, позволяющим наглядно и детально описывать параллельные процессы, является теория сетей Петри. Сети Петри позволяют убедиться в логической корректности алгоритма функционирования системы, достижимости некоторого состояния, найти тупиковые состояния и другие характеристики.
Сети Петри применяются от юриспруденции и биологии до теории надежности и проектирования робастных систем.
Предоставление реальной системы в виде сетей Петри- это формальная и наглядная запись алгоритма ее функционирования.
Сеть Петри - направленный двудольный граф, в котором есть кроме ребер (стрелочки) два вида вершин.
Это переходы:

и позиции (условия):
| |||
 |
Внутри позиции может помещаться одна или несколько меток (маркеров). Графически сеть Петри изображается диаграммой переходов состояний.
tj- имеет возможность срабатывания, если входы в переход имеют по меньшей мере один маркер. Если tj срабатывает, то при удалении по одному символу из всех входов в переход tj осуществляется подача символов по одному на все выходы. Это правило реализации сети Петри, то есть динамическая характеристика моделируемой системы, возможности срабатывания элементов.
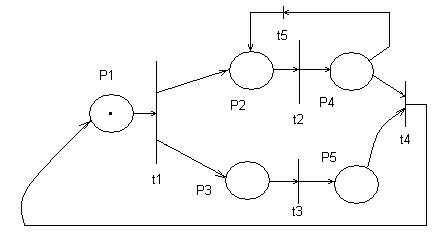
Структура сетей Петри описывается векторами позиций:
P={P1,P2,P3,P4,P5}
и переходов:
T={t1,t2,t3,t4,t5},
а также векторами позиций и переходов системы связей со входа и выхода переходов:
I(t1)={P1} O(t1)={P2;P3}
I(t2)={P2} O(t2)={P4}
I(t3)={P3} O(t3)={P5}
I(t4)={P4;P5} O(t4)={P1}
I(t5)={P4} O(t5)={P2}
Динамика сетей Петри зависит от исходной разметки позиции:
μ=μ0(1,0,0,0,0).

 μ0:(1,0,0,0,0)
μ0:(1,0,0,0,0)
 t1
t1
μ1:(0,1,1,0,0) t4
t2,t3
 μ2:(0,0,0,1,1) μ:(1,0,0,0,0)
μ2:(0,0,0,1,1) μ:(1,0,0,0,0)


 t2
t2
t5
 μ3:(0,1,0,0,1) μ:(0,0,0,1,1)
μ3:(0,1,0,0,1) μ:(0,0,0,1,1)
Динамика срабатывания схемы отображается на ней в виде копии структуры в позициях, в которых маркер будет переходить с позиции на позицию.
То есть последовательность срабатывания данной сети Петри может отражаться последовательностью векторов разметки.
Сеть Петри называется активной, если все переходы в сетях Петри могут сработать при смене состояний от μ0 до μконечного, символы появятся во всех позициях. Тупиковое состояние - случай, когда при всех разметках какой-то переход не может сработать. Если в сетях Петри возникло тупиковое состояние, значит либо при моделировании, либо при описании образовалась ошибка, следовательно, необходимы повторные исследования.
Дата добавления: 2021-11-16; просмотров: 624;











