Глава 3. Интерполирование и аппроксимация функций, заданных таблично

Основные понятия

В данной главе рассматривается случай табличного задания функции одной переменной. С математической точки зрения это означает, что значения функции f(x) на промежутке [a, b] заданы в узлах одномерной сетки

h_x = {x_i / x_i = x_{i – 1} + h_i, h_i > 0, i = 1, 2, 3, …, n; x₀ = a, x_n = b}, (3.1.1)

где x_i, i = 0, 1, 2, …, n – узлы одномерной сетки h_x; h_i, i = 1, 2, 3, …, n – шаг сетки h_x. Если h_i = h " i = 1, 2, 3, …, n, сетка h_x равномерная.

В случае табличного задания функции на отрезке [a, b]часто возникает проблема восстановления значений функции f(x) в произвольной точке x Î (a, b) между узлами сетки h_x. Такую задачу называют задачей интерполирования (или интерполяции) значений функции в точку x Î (a, b).

Наряду с задачей интерполяции значений функции решается задача определения возможных значений таблично заданной на отрезке [a, b] функции f(x) в точках, не принадлежащих этому отрезку. Эту задачу также называют задачей экстраполяции значений функции в точку x Ï [a, b].

В более общей постановке ставится задача замены таблично заданной на отрезке [a, b] функции f(x) некоторой функцией j (x) из заданного класса функций (например, полиномов той или иной степени, экспоненциальных функций и т. д.). При этом выбор функции j (x) из заданного класса осуществляется таким образом, чтобы ее значения были в наибольшей степени согласованы в смысле некоторого критерия с табличными данными. Такая задача называется задачей аппроксимации или приближения таблично заданных функций. Формально задачи интерполяции и экстраполяции таблично заданной функции решаются посредством аппроксимации ее функциями заданного класса.

Рассмотрим некоторые методы решения задач интерполяции.

Приведем формальную постановку задачи полиномиальной интерполяции таблично заданной на отрезке [a, b] функции f(x). Пусть на отрезке [a, b] задана одномерная сетка

h_x = {x_i / x_i = x_{i – 1} + h_i, h_i > 0, i = 1, 2, 3, …, n; x₀ = a, x_n = b},

в узлах x_i которой заданы y_i = f(x_i), i = 0, 1, 2, …, n – соответствующие значения функции f(x).

Функция j (x) называется интерполирующей или интерполяционной для f(x) на [a, b], если ее значения j (x₀), j (x₁), …, j (x_n) в узлах сетки
x₀, x₁, x₂,…, x_n совпадают с заданными значениями y_i функции f(x_i), i = 0, 1, 2, …, n. Геометрически это означает, что график функции j (x) проходит так, что по крайней мере в точке (n + 1) (в точках, соответствующих узлам сетки h_x) на отрезке [a, b] он пересекает или касается истинного графика функции f(x).

Пусть в качестве интерполяционной функции j (x) выбран полином P_n(x) – алгебраический многочлен степени n:

P_n(x) = a₀ + a₁x + a₂x² + … + a_nxⁿ.

Тогда задача полиномиальной интерполяции формулируется так: для функции f(x), заданной таблично, определить полином P_n(x), при котором выполняются условия

P_n(x_i) = y_i , i = 0, 1, 2, …, n. (3.1.2)

Для того чтобы определить полином, необходимо найти значения
его (n + 1) коэффициента: a₀, a₁, a₂, …, a_n. Для этого имеется (n + 1) условие (3.1.2). Иначе говоря, для того чтобы полином был интерполяционным для таблично заданной функции f(x), достаточно, чтобы его коэффициенты удовлетворяли системе уравнений

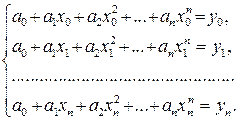(3.1.3)

Поскольку все узлы сетки h_x различны (h_i > 0 "i), то определитель этой системы (определитель Вандермонда) отличен от нуля, следовательно, решение системы (3.1.3) существует и является единственным. Таким образом, чтобы построить интерполяционный полином P_n(x), нужно составить систему линейных уравнений (3.1.3). Ее решение позволит определить значения коэффициентов полинома, удовлетворяющего условиям (3.1.2). Из единственности решения системы (3.1.3) следует единственность интерполяционного полинома P_n(x). Зная интерполяционный полином, можно определить его значение P_n(x^*) в любой, не совпадающей с узлами сетки h_x точке x^* Î (a, b), осуществив тем самым интерполяцию таблично заданной функции f(x) в точку x^*.

Рассмотренный способ построения интерполяционного полинома
с практической точки зрения не всегда эффективен. Существуют альтернативные способы его построения, не требующие решения системы линейных уравнений (3.1.3). Эти способы более подробно рассмотрены в § 3.2 и 3.3.

Существенным недостатком полиномиальной интерполяции является то, что при большом числе узлов сетки степень полинома P_n(x), определяемого на отрезке [a, b], будет большой. Известно, что полиномы с большими степенями крайне неустойчиво ведут себя в промежутках между узлами сетки h_x, часто принимая там неоправданно большие по абсолютной величине значения, заведомо не соответствующие возможным значениям функции f(x). Поэтому на практике не рекомендуется строить интерполяционные полиномы выше 5-6-й степени.

В связи с этим при большом количестве узлов сетки h_x целесообразно
либо строить интерполяционный полином для небольшой части узлов сетки, находящихся на оси Ох с обеих сторон от точки, в которую предполагается интерполировать данные, либо применять неполиномиальную интерполяцию таблично заданных функций. Широкое распространение получили методы интерполяции так называемыми сплайнами. Пример постановки и решения задачи сплайн-интерполяции приведен в § 3.4.

Рассмотрим другую формальную постановку задачи аппроксимации таблично заданной функции функцией из заданного класса. Пусть, как и ранее, на отрезке [a, b] задана одномерная сетка

h_x = {x_i / x_i = x_{i – 1} + h_i, h_i > 0, i = 1, 2, 3, …, n; x₀ = a, x_n = b},

в узлах x_i которой заданы y_i = f(x_i), i = 0, 1, 2, …, n – соответствующие значения функции f(x).Из заданного класса функций требуется найти такую функцию j (x, с) (где c Î Е_m – вектор определяемых параметров), чтобы суммарное отклонение значений функции j (x) в узлах сетки h_x от заданных в этих узлах значений функции f(x) было минимальным. Для оценки суммарного отклонения может быть использован, например, критерий метода наименьших квадратов:

F(j (x, c)) = [f(x_k) – j (x_k, c)]² Þ min. (3.1.4)

В данной постановке задачи (в отличие от рассмотренной ранее задачи интерполяции) не требуется обязательного совпадения значений аппроксимирующей и таблично заданной функций в узлах сетки h_x. В принципе такое совпадение, конечно, может иметь место. В этом случае критерий (3.1.4) окажется равным нулю для построенной функции j (x, с), а сама функция будет интерполяционной. Таким образом, рассмотренная постановка аппроксимации таблично заданной функции является обобщением обсуждавшейся ранее задачи интерполяции.

В целом рассмотренная более общая постановка аппроксимации табличных данных является целесообразной. Например, когда табличные данные имеют достаточно большую погрешность и интерполяция по ним, очевидно, теряет смысл. Кроме того, такая аппроксимация оказывается полезной при необходимости так называемого "сглаживания" табличных данных с целью выделения некоторого низкочастотного тренда, характеризующего качественную тенденцию поведения табличных данных, а также при решении ряда других прикладных исследовательских задач.

Более подробно задача аппроксимации таблично заданной функции методом наименьших квадратов рассматривается в § 3.5.