Полярные координаты и их связь с декартовыми. Геометрический смысл уравнений и неравенств с двумя переменными. Окружность и ее уравнение
Основные теоретические сведения
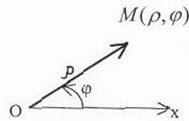
Полярная система координат определяется заданием некоторой точки 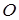 , луча
, луча 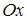 , исходящего из этой точки, и единицы масштаба (рис. 2.25). Точка
, исходящего из этой точки, и единицы масштаба (рис. 2.25). Точка 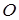 называется полюсом, а луч
называется полюсом, а луч 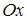 – полярной осью.
– полярной осью.
Если 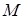 – произвольная точка плоскости, не совпадающая с полюсом, то ее положение на плоскости определяется заданием двух чисел: расстоянием
– произвольная точка плоскости, не совпадающая с полюсом, то ее положение на плоскости определяется заданием двух чисел: расстоянием 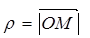 от полюса и углом
от полюса и углом 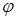 между полярной осью и вектором
между полярной осью и вектором 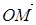 . Угол
. Угол 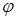 называется полярным углом, а расстояние
называется полярным углом, а расстояние 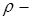 полярным радиусом точки
полярным радиусом точки 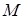 . Полярный радиус
. Полярный радиус 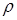 и полярный угол
и полярный угол 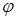 точки
точки 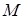 называют ее полярными координатами и записывают
называют ее полярными координатами и записывают 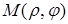 .
.
В определенной таким образом полярной системе координат, полярный радиус 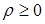 , а угол
, а угол 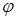 заключен в пределах
заключен в пределах 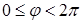 либо
либо 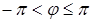 . Числа
. Числа 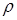 и
и 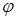 определяют положение единственной точки на плоскости, и обратно, каждой точке плоскости однозначно отвечает пара чисел
определяют положение единственной точки на плоскости, и обратно, каждой точке плоскости однозначно отвечает пара чисел 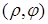 . Исключение составляет только полюс, для которого
. Исключение составляет только полюс, для которого 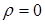 , а угол
, а угол 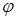 не определен.
не определен.
| 
|
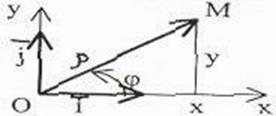
Рис. 2.25 Рис. 2.26
Если выбрать декартову систему координат так, чтобы ее начало О совпало с полюсом, а ось Ox - с полярной осью (рис. 2.26), то между полярными координатами 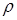 ,
, 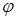 и декартовыми координатами x, y каждой точки М существует следующая связь:
и декартовыми координатами x, y каждой точки М существует следующая связь:
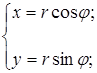 (5.1)
(5.1)
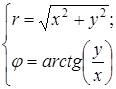 (5.2)
(5.2)
с учетом четверти, в которой находится число.
Из этих формул следует:
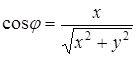 ;
; 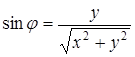 . (5.3)
. (5.3)
В аналитической геометрии всякую линию на плоскости рассматривают как множество точек, обладающих каким-то свойством, общим для всех ее точек. Следовательно, обозначив через 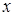 и
и 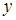 или
или 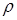 и
и 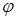 координаты произвольной точки рассматриваемой линии в соответствующей системе координат, выражают посредством уравнения относительно
координаты произвольной точки рассматриваемой линии в соответствующей системе координат, выражают посредством уравнения относительно 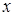 и
и 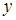 или
или 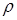 и
и 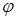 свойство, общее для всех точек линии.
свойство, общее для всех точек линии.
Таким образом, уравнением данной линии называется такое уравнение относительно переменных 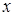 и
и 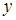 или
или 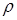 и
и 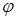 , которому удовлетворяют координаты любой точки, лежащей на этой линии, и не удовлетворяют координаты ни одной точки, не лежащей на ней.
, которому удовлетворяют координаты любой точки, лежащей на этой линии, и не удовлетворяют координаты ни одной точки, не лежащей на ней.
Координаты 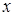 и
и 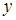 или
или 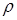 и
и 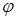 , входящие в уравнение линии, называются текущими координатами.
, входящие в уравнение линии, называются текущими координатами.
Принято говорить, что уравнение 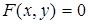 или
или 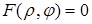 определяют линию на плоскости. Однако следует заметить, не любое уравнение
определяют линию на плоскости. Однако следует заметить, не любое уравнение 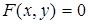 определяет линию на плоскости. Например, уравнению
определяет линию на плоскости. Например, уравнению 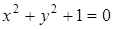 не удовлетворяют координаты ни одной точки.
не удовлетворяют координаты ни одной точки.
Неравенство с двумя переменными 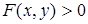 или
или 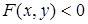 определяет множество точек плоскости, представляющее собой какую-то область. Следует заметить, что множество точек плоскости, координаты которых удовлетворяют некоторому неравенству, может быть пустым. Например, неравенство
определяет множество точек плоскости, представляющее собой какую-то область. Следует заметить, что множество точек плоскости, координаты которых удовлетворяют некоторому неравенству, может быть пустым. Например, неравенство 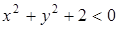 определяет пустое множество. Наоборот, неравенству
определяет пустое множество. Наоборот, неравенству 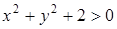 удовлетворяют координаты любой точки плоскости.
удовлетворяют координаты любой точки плоскости.
Очень часто линию на плоскости удобно задавать не одним уравнением 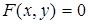 , а системой уравнений, в которой каждая текущая координата задается некоторой функцией от одного и того же аргумента, например
, а системой уравнений, в которой каждая текущая координата задается некоторой функцией от одного и того же аргумента, например 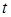 , называемого параметром. Получают уравнение вида
, называемого параметром. Получают уравнение вида
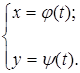 (5.4)
(5.4)
Уравнения (5.4) называются параметрическими уравнениями линии на плоскости. При одном и том же значении параметра 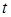 уравнения (5.4) определяют координаты
уравнения (5.4) определяют координаты 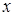 и
и 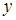 некоторой точки линии.
некоторой точки линии.
Дата добавления: 2017-09-01; просмотров: 2131;











