Задание для самостоятельной работы
1. Определите полуоси, координаты фокусов и эксцентриситет эллипса 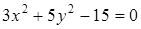 .
.
Ответ: 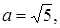
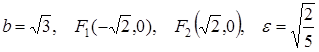 .
.
2. Составьте каноническое уравнение эллипса, у которого малая полуось равна 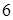 , а расстояние между фокусами равно
, а расстояние между фокусами равно 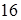 .
.
Ответ: 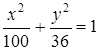 .
.
3. Составьте каноническое уравнение эллипса, у которого большая полуось равна 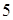 , а эксцентриситет равен
, а эксцентриситет равен 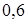 .
.
Ответ: 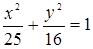 .
.
4. Эллипс касается оси абсцисс в вершине 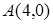 и оси ординат в вершине
и оси ординат в вершине 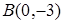 . Составьте уравнение этого эллипса.
. Составьте уравнение этого эллипса.
Ответ: 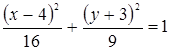 .
.
5. Определите траекторию точки 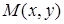 , которая при своем движении остается в два раза ближе к точке
, которая при своем движении остается в два раза ближе к точке 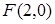 , чем к прямой
, чем к прямой 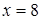 .
.
Ответ: 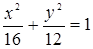 .
.
6. Оси эллипса совпадает с осями координат, и эллипс проходит через точки 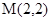 ,
, 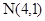 . Составьте уравнение этого эллипса.
. Составьте уравнение этого эллипса.
Ответ: 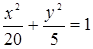 .
.
7. Составьте уравнение гиперболы, имеющей вершины в фокусах, а фокусы – в вершинах эллипса 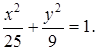
Ответ: 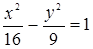 .
.
8. Составьте каноническое уравнение гиперболы, если ее фокусы лежат на оси 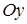 и расстояние между ними равно
и расстояние между ними равно 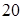 , а действительная ось гиперболы равна 16.
, а действительная ось гиперболы равна 16.
Ответ: 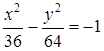 .
.
9.Найдите длины осей, координаты фокусов, эксцентриситет и уравнения асимптот гиперболы 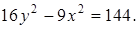
Ответ: 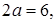
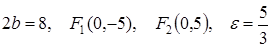 .
.
10. Составьте каноническое уравнение гиперболы, зная, что расстояние между фокусами равно 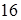 , а эксцентриситет
, а эксцентриситет 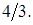
Ответ: 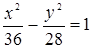 .
.
11. Составьте уравнение гиперболы, если известно, что асимптоты заданы уравнениями 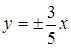 и гипербола проходит через точку
и гипербола проходит через точку 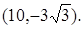
Ответ: 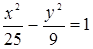 .
.
12. Определите траекторию точки 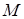 , которая при своем движении остается вдвое ближе к прямой
, которая при своем движении остается вдвое ближе к прямой 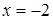 , чем к точке
, чем к точке 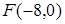 .
.
Ответ: 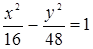 .
.
13. Составьте уравнение гиперболы, если известно, что ее асимптоты заданы уравнениями 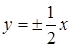 и расстояние между фокусами равно
и расстояние между фокусами равно 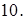
Ответ: 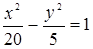 .
.
14.Парабола симметрична относительно оси 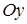 , проходит через точку
, проходит через точку 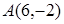 , а вершина ее лежит в начале координат. Составьте уравнение этой параболы.
, а вершина ее лежит в начале координат. Составьте уравнение этой параболы.
Ответ: 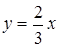 .
.
15. Найдите уравнение директрисы и фокус параболы 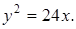
Ответ: 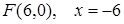 .
.
16. Парабола с вершиной в начале координат проходит через точку 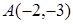 и симметрична относительно оси
и симметрична относительно оси 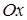 . Составьте ее уравнение и найдите фокус и директрису.
. Составьте ее уравнение и найдите фокус и директрису.
Ответ: 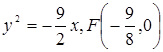 .
.
17. Струя воды, выбрасываемая фонтаном, принимает форму параболы, параметр которой 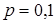 . Определите высоту струи, если известно, что она падает в бассейн на расстоянии
. Определите высоту струи, если известно, что она падает в бассейн на расстоянии 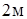 от места выхода.
от места выхода.
Ответ: 5 м.
18. Составьте уравнение множества центров окружностей, касающихся оси 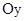 и окружности
и окружности 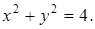
Ответ: 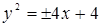 .
.
19. Составьте уравнение середины хорд параболы 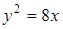 , проходящих через ее фокус.
, проходящих через ее фокус.
Ответ: 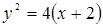 .
.
20. Выделением полных квадратов и переносом начала координат упростите уравнения линий и постройте их:
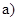
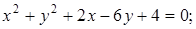
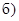
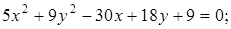
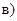
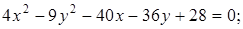
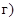
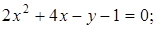
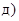
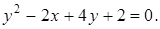
Ответ: а) 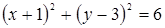 ; г)
; г) 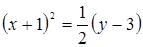 ;
;
б) 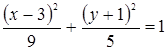 ; д)
; д) 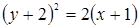 .
.
в) 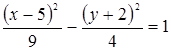 ;
;
21. Приведите к каноническому виду уравнения линий второго порядка. Установите тип этих линий и их расположение:
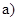
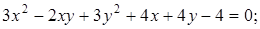
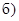
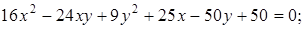
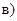
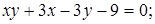
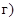
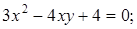
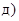
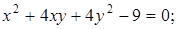
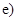
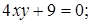
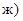
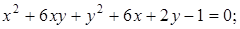
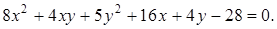
Ответ: а) 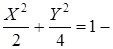 эллипс; д)
эллипс; д) 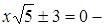 пара прямых;
пара прямых;
б) 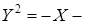 парабола; е)
парабола; е) 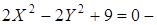 равностор.гиперб.;
равностор.гиперб.;
в) 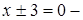 пара прямых; ж)
пара прямых; ж) 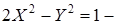 гипербола;
гипербола;
г) 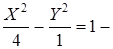 гипербола; з)
гипербола; з) 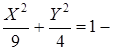 эллипс.
эллипс.
22. Найдите траекторию точки, которая движется так, что расстояние от нее до точки 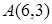 вдвое меньше, чем до точки
вдвое меньше, чем до точки 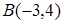 .
.
Ответ: 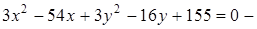 окружность.
окружность.
23. Даны окружность 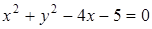 и точка
и точка 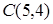 . Составьте уравнение окружности, имеющий центр в данной точке и касающейся данной окружности внешним образом.
. Составьте уравнение окружности, имеющий центр в данной точке и касающейся данной окружности внешним образом.
Ответ: 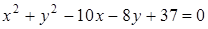 .
.
24. Составьте уравнение окружности, проходящей через точки 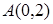 ,
, 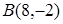 и
и 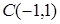 .
.
Ответ: 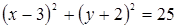 .
.
25. В эллипс 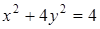 вписан правильный треугольник, одна из вершин которого совпадает с концом большой полуоси. Определите координаты двух других вершин треугольника.
вписан правильный треугольник, одна из вершин которого совпадает с концом большой полуоси. Определите координаты двух других вершин треугольника.
Ответ: 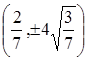 .
.
26. Составьте уравнения множества точек, отношение расстояний, от которых до данной точки 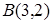 и данной прямой
и данной прямой 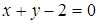 равно
равно 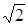 . Сделайте чертеж.
. Сделайте чертеж.
Ответ: 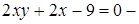 равносторонняя гипербола.
равносторонняя гипербола.
27. Определите множество центров окружности, касающихся окружности 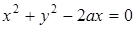 и оси
и оси 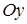 .
.
Ответ: 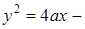 парабола.
парабола.
28. Найдите длину хорды, соединяющие точки пересечения двух парабол, имеющих общую вершину в начале координат и фокусы в точках 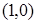 и
и 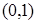 .
.
Ответ: 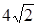 .
.
29. Ракета, пуск которой произведен под острым углом, описала дугу параболы и упала на расстоянии 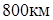 от начального положения. Определите параметр параболической траектории, если наибольшая высота, достигнутая ракетой, равна
от начального положения. Определите параметр параболической траектории, если наибольшая высота, достигнутая ракетой, равна 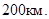
Ответ: 400.
30. В параболу 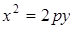 вписан равносторонний треугольник, одна из вершин которого совпадает с вершиной параболы. Найдите длину стороны треугольника.
вписан равносторонний треугольник, одна из вершин которого совпадает с вершиной параболы. Найдите длину стороны треугольника.
Ответ: 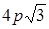 .
.
31. Постройте кривые, заданные уравнениями:
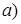
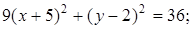
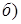
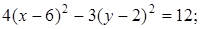
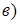
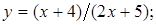
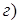
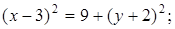
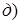
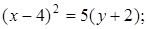
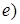
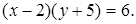
Дата добавления: 2017-09-01; просмотров: 2737;











