Задание для самостоятельной работы
1.В полярной системе координат постройте точки 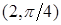 ,
, 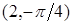 ,
, 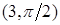 ,
, 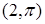 ,
, 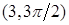 ,
, 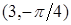 .
.
2. В полярной системе координат даны точки 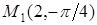 ,
, 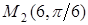 ,
, 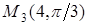 ,
, 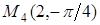 .Найдите их декартовы координаты, совместив декартову прямоугольную систему координат с полярной, поместив начало координат в точки полюса и направив полярную ось в положительном направлении оси Ох.
.Найдите их декартовы координаты, совместив декартову прямоугольную систему координат с полярной, поместив начало координат в точки полюса и направив полярную ось в положительном направлении оси Ох.
Ответ. 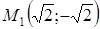 ,
, 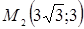 ,
, 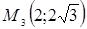 ,
, 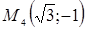 .
.
3. Запишите в полярных координатах уравнения кривых и постройте эти кривые: а) 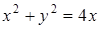 ; б)
; б) 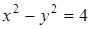 ; в)
; в) 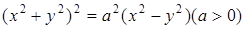 .
.
Ответ: а) 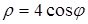 ; б)
; б) 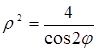 ; в)
; в) 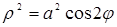 .
.
4. Составьте параметрические уравнения окружности, радиус которой 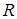 , а центр находится в начале координат.
, а центр находится в начале координат.
Ответ. 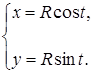
5. Приведите к виду 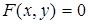 или
или 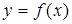 уравнения кривых, заданных параметрически:
уравнения кривых, заданных параметрически:
а) 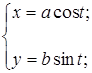 б)
б) 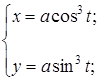 в)
в) 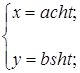 г)
г) 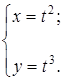
Ответ: а) 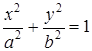 , б)
, б) 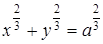 , в)
, в) 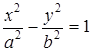 , г)
, г) 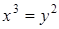 .
.
6. Определите траекторию точки 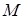 , которая при своем движении все время остается вдвое ближе к точке
, которая при своем движении все время остается вдвое ближе к точке 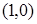 , чем к точке
, чем к точке 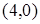 .
.
Ответ: 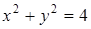 .
.
7. Определите траекторию точки, которая при своем движении остается в двое дальше от точки 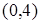 , чем от прямой
, чем от прямой 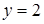 .
.
Ответ: 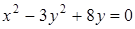 .
.
Кривые второго порядка
Эллипс
Основные теоретические сведения
Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных точек 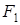 и
и 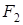 , называемых фокусами эллипса, есть величина постоянная (большая, чем расстояние между фокусами).
, называемых фокусами эллипса, есть величина постоянная (большая, чем расстояние между фокусами).
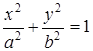 ,
,
где 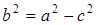
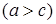 . В этом случае фокусы эллипса
. В этом случае фокусы эллипса 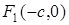 ,
, 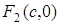 (рис.2.31).
(рис.2.31).
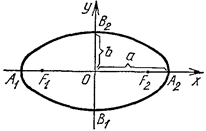 Рис. 2.31
Рис. 2.31
| Начало координат  является центром симметрии эллипса, а оси координат – осями симметрии эллипса. Точки является центром симметрии эллипса, а оси координат – осями симметрии эллипса. Точки 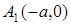 , , 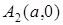 , , 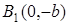 , , 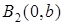 называются вершинами эллипса, а длины отрезков называются вершинами эллипса, а длины отрезков 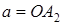 и и 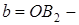 соответственно большой и малой полуосями. соответственно большой и малой полуосями.
|
Таким образом, эллипс есть замкнутая выпуклая линия с двумя осями симметрии и центром симметрии (рис. 2.31).
Величина 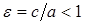 называется эксцентриситетом эллипса.
называется эксцентриситетом эллипса.
Окружность можно считать частным случаем эллипса, у которого 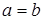 , т.е.
, т.е. 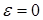 .
.
Уравнение эллипса с осями симметрии, параллельными координатным осям, имеет вид
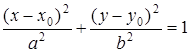 ,
,
где 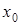 ,
, 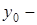 координаты центра симметрии эллипса.
координаты центра симметрии эллипса.
Гипербола
Гиперболой называется множество точек плоскости, модуль разности расстояний от которых до двух данных точек 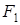 и
и 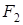 , называемых фокусами гиперболы, есть величина постоянная (не равная нулю и меньшая, чем расстояние между фокусами).
, называемых фокусами гиперболы, есть величина постоянная (не равная нулю и меньшая, чем расстояние между фокусами).
Если обозначить постоянную величину через 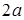 , а расстояние между фокусами через , а расстояние между фокусами через 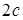 и выбрать систему координат так же, как и для эллипса (рис. 2.32), то уравнение гиперболы примет канонический вид и выбрать систему координат так же, как и для эллипса (рис. 2.32), то уравнение гиперболы примет канонический вид 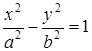 ,
где ,
где 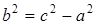 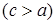 . .
| 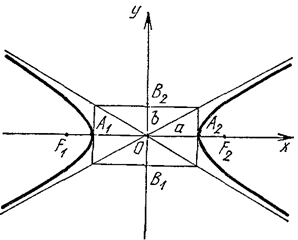 Рис. 2.32
Рис. 2.32
|
В этом случае фокусы гиперболы 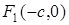 и
и 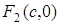 . Оси координат являются осями симметрии гиперболы, а точка
. Оси координат являются осями симметрии гиперболы, а точка 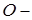 ее центром симметрии. Гипербола пересекает ось абсцисс в точках
ее центром симметрии. Гипербола пересекает ось абсцисс в точках 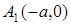 и
и 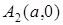 , которые называются действительными вершинами, а величина
, которые называются действительными вершинами, а величина 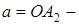 действительной полуосью гиперболы. Точки
действительной полуосью гиперболы. Точки 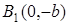 и
и 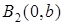 называются мнимыми вершинами гиперболы, а величина
называются мнимыми вершинами гиперболы, а величина 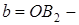 мнимой полуосью.
мнимой полуосью.
Прямоугольник с центром в начале координат и сторонами, параллельными координатным осям и проходящими через вершины гиперболы, называется основным прямоугольником гиперболы.
Гиперболы имеют две асимптоты, т.е. прямые, к которым неограниченно приближаются ветви гиперболы. Уравнения асимптот:
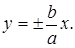
Отсюда следует, что они являются диагоналями основного прямоугольника. Для построения гиперболы всегда лучше сначала построить ее асимптоты, а затем уже саму кривую.
Эксцентриситет гиперболы 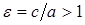 . Выражая эксцентриситет через полуоси гиперболы:
. Выражая эксцентриситет через полуоси гиперболы:
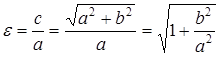 ,
,
видим, что он характеризует вытянутость основного прямоугольника гиперболы.
Уравнение гиперболы с осями симметрии, параллельными координатным осям, имеет вид
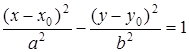 ,
,
где 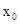 ,
, 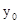 - координаты центра гиперболы.
- координаты центра гиперболы.
Если оси гиперболы равны, т.е. 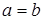 , гипербола называется равносторонней. Ее уравнение имеет вид
, гипербола называется равносторонней. Ее уравнение имеет вид
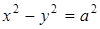 .
.
Для равносторонней гиперболы основной прямоугольник превращается в квадрат, а эксцентриситет равен 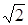 .
.
Парабола
Параболой называется множество точек плоскости, равноудаленных от данной точки 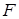 , называемой фокусом параболы, и данной прямой
, называемой фокусом параболы, и данной прямой 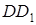 , называемой ее директрисой.
, называемой ее директрисой.
Если выбрать прямоугольную систему координат так, чтобы ось 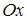 проходила через фокус
проходила через фокус 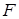 и была перпендикулярна к директрисе
и была перпендикулярна к директрисе 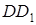 , а ось
, а ось 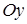 проходила между фокусом и директрисой (рис. 2.33), то уравнение параболы примет канонический вид
проходила между фокусом и директрисой (рис. 2.33), то уравнение параболы примет канонический вид
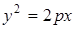 ,
,
где 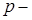 расстояние от фокуса до директрисы. Уравнение директрисы
расстояние от фокуса до директрисы. Уравнение директрисы 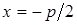 , фокус
, фокус 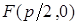 .
.
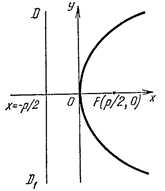 Рис. 2.33
Рис. 2.33
| 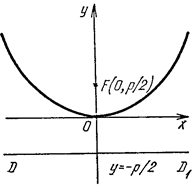 Рис. 2.34
Рис. 2.34
|
Начало координат является вершиной параболы, а ось абсцисс – ее осью симметрии. Эксцентриситет параболы 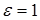 .
.
Если осью симметрии параболы служит ось ординат (рис. 2.34), то уравнение параболы имеет вид
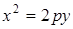
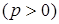 .
.
Уравнение директрисы в этом случае 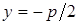 , фокус
, фокус 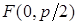 .
.
Уравнение параболы с осью симметрии, параллельной одной из координатных осей, имеет вид
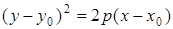 или
или 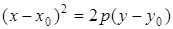 ,
,
где 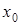 ,
, 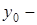 координаты вершины параболы.
координаты вершины параболы.
Дата добавления: 2017-09-01; просмотров: 1709;











