Линии второго порядка.

Уравнение одной и той же линии может иметь различный вид в зависимости от того, как будет расположена система координат, к которой отнесена кривая. С помощью преобразования координат можно привести это уравнение к простейшему (каноническому) виду.

Общее уравнение линии второго порядка имеет вид

,

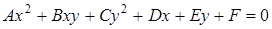либо

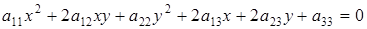. (6.1)

Определитель

,

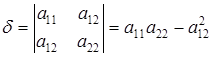называют дискриминантом старших членов уравнения (6.1).

Если 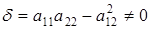, то линия, задаваемая уравнением (6.1), имеет единственный центр симметрии и называется центральной линией, а ее центр симметрии – просто центром. Остальные линии носят название нецентральных. Примеры центральной линии – эллипс, гипербола, а нецентральной – парабола.

Если уравнение (6.1) задает центральную линию, то можно осуществить параллельный перенос осей координат по формулам

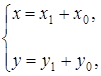
где 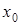, 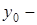координаты нового начала 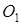, являющегося центром линии. Они определяются из системы

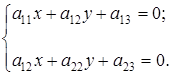
В новой системе 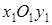уравнение (6.1) приводится к виду

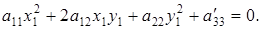(6.2)

Из уравнения (6.2) заключаем, что коэффициенты при старших членах в результате параллельного переноса не изменяются, а свободный член

,

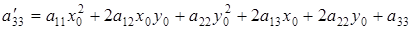т.е. свободный член при параллельном переносе равен результату подстановки в левую часть уравнения (6.1) вместо текущих координат 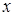, 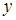координат нового начала , .

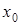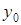Для дальнейшего упрощения уравнения (6.2) применим правило приведения квадратичной формы к каноническому виду, т.е. если повернем оси координат так, чтобы направления осе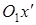й и 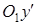совпадали с главными направлениями квадратичной формы, то уравнение приведется к каноническому виду:

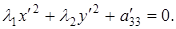(6.3)

где 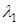, 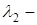корни характеристического уравнения

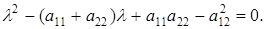(6.4)

Если 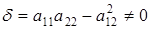, то согласно теореме Виета, из уравнения (6.4) следует, что 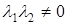, т.е. характеристические числа 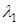и 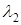отличны от нуля.

Возможны два случая.

1. Числа 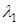и 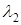одного знака, следовательно, 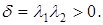Если свободный член 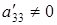и его знак противоположен знаку чисел 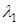, , 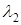уравнение (6.3) определяет эллипс. Если же знак члена 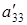совпадает со знаком чисел 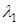, , 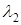уравнение (6.3) не имеет смысла (мнимый эллипс). При 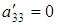уравнение (6.3) определяет одну вещественную точку 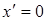и .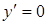

2. Числа 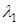и 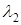разных знаков, следовательно, 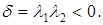В этом случае, если 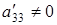, уравнение (6.3) определяет гиперболу, если же 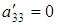, – пару пересекающихся прямых.

Рассмотрим теперь случай, когда уравнение (6.1) определяет нецентральную линию, т.е. когда

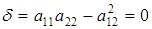. (6.5)

Так как 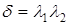, то в силу условия (6.5) хотя бы одно из чисел 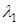, 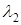равно нулю. Для определенности возьмем 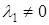, 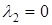. Выполним поворот системы координат 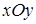так, чтобы направления новых осе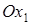й и 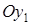совпали с главными направлениями квадратичной формы старших членов уравнения (6.1) (в новой системе координат ось 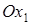совпадает с главным направлением, соответствующим характеристическому числу 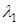). Тогда уравнение (6.1) в системе 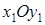примет вид

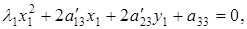(6.6)

где

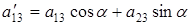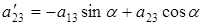; . (6.7)

При исследовании геометрического смысла уравнения (6.6) возможны следующие случаи:

1) коэффициент 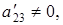тогда уравнение (6.6) определяет параболу, ось симметрии которой параллельна оси ;

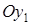2) коэффициент 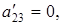тогда уравнение (6.6) определяет пару параллельных прямых (действительных, если дискриминант 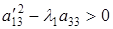; совпадающих, если 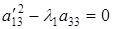, и мнимых, если ).

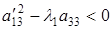Таким образом, уравнение (6.1) при 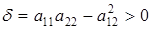определяет действительный или мнимый эллипс либо точку 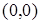, при 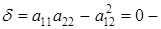параболу либо пару параллельных прямых, при 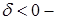гиперболу или пару пересекающихся прямых.