Поверхности второго порядка
Цилиндрические и конические поверхности.
Поверхности вращения
Основные теоретические сведения
Цилиндрической поверхностью или просто цилиндром называется всякая поверхность, которую можно получить движением прямой, перемещающийся параллельно некоторому вектору и все время пересекающей данную линию, которая носит название направляющей. Движущаяся прямая называется образующей.
Конической поверхностью или просто конусом называется поверхность, образованная движением прямой, проходящей через данную точку, называемую вершиной конуса, и скользящей по данной кривой. Движущаяся прямая называется образующей конуса, а кривая, по которой скользит образующая, - направляющей.
Вращением фигуры  вокруг данной прямой (оси вращения) называется такое движение, при котором каждая точка фигуры
вокруг данной прямой (оси вращения) называется такое движение, при котором каждая точка фигуры  описывает окружность с центром на оси вращения, лежащую в плоскости, перпендикулярной к оси вращения.
описывает окружность с центром на оси вращения, лежащую в плоскости, перпендикулярной к оси вращения.
Поверхность, образованная вращением линии вокруг оси, называется поверхностью вращения.
Канонические уравнения поверхностей
Второго порядка
Поверхность второго порядка задается в прямоугольных координатах уравнением второй степени
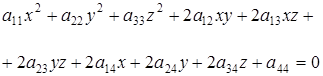 (7.1)
(7.1)
Путем преобразования координат (поворотом осей и параллельным переносом) уравнение (7.1) приводится к каноническому виду. В случае, когда в уравнении (7.1) отсутствуют члены с произведением координат 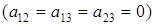 , это уравнение выделением полных квадратов по
, это уравнение выделением полных квадратов по 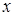 ,
, 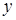 ,
, 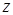 и параллельным переносом осей координат приводится к каноническому виду подобно тому, как это делалось для линий второго порядка (см. Исследование общего уравнение линии второго порядка). Поверхности второго порядка и их канонические уравнения представлены в табл. 3.
и параллельным переносом осей координат приводится к каноническому виду подобно тому, как это делалось для линий второго порядка (см. Исследование общего уравнение линии второго порядка). Поверхности второго порядка и их канонические уравнения представлены в табл. 3.
Форму и расположение поверхностей второго порядка обычно изучают методом параллельных сечений. Сущность метода заключается в том, что поверхность пересекается несколькими плоскостями, параллельными координатным плоскостям. Форма и параметры полученных сечений позволяют выяснить форму самой поверхности.
Таблица 3
| Поверхность второго порядка, каноническое уравнение | Вид |
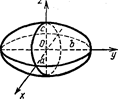
Эллипсоид
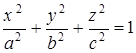
| 
|
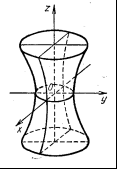
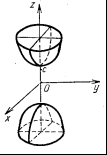
Гиперболоид:
однополостный,
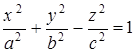 двуполостный,
двуполостный,
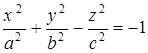
| 
|
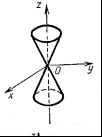
Конус,
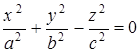
| 
|
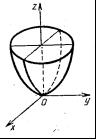
Параболоид:
эллиптический, 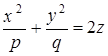 гиперболический,
гиперболический, 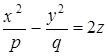
| 
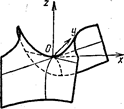
|
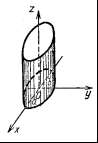
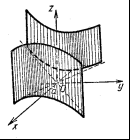
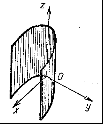
Цилиндр:
эллиптический, 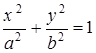 гиперболический,
гиперболический, 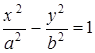 параболический,
параболический, 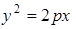
| 
|
Дата добавления: 2017-09-01; просмотров: 1626;











