Построить точки, заданные своими полярными координатами
Задача 5.1. Построить точки, заданные своими полярными координатами: 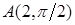 ,
, 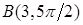 ,
, 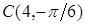 .
.
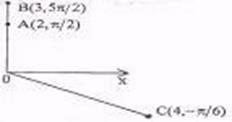
Решение. Построение точек показано на рис. 2.27.
 |
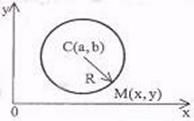 |
Рис. 2.27 Рис. 2.28
Задача 5.2. В полярной системе координат даны точки 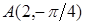 ,
, 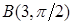 ,
, 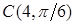 . Найти их декартовы координаты, выбрав декартову систему координат так, как показано на рис. 2.28.
. Найти их декартовы координаты, выбрав декартову систему координат так, как показано на рис. 2.28.
Решение. Подставив полярные координаты в формулы (5.1) найдем, декартовы координаты данных точек: 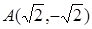 ,
, 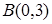 ,
, 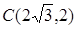 .
.
Ответ. 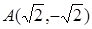 ,
, 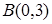 ,
, 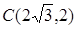 .
.
Задача 5.3.Составить уравнение окружности, радиус которой 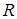 , а центр находится в точке
, а центр находится в точке 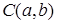 (рис. 2.28).
(рис. 2.28).
Решение. Окружностью называется множество точек плоскости, находящихся на одном и том же расстоянии 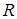 от центра.
от центра.
Обозначив через 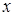 и
и 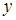 координаты произвольной точки
координаты произвольной точки 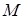 окружности и выразив через них равенство
окружности и выразив через них равенство 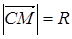 , получим
, получим
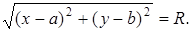 (5.5)
(5.5)
Возведя в квадрат обе части равенства (5.5), придадим ему более удобную форму:
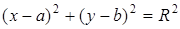 . (5.6)
. (5.6)
Очевидно, что это соотношение выполнено для всех точек окружности, и только для них, следовательно, его можно рассматривать как запись определения окружности с помощью координат. Равенство (5.5) называется уравнением окружности в рассматриваемой системе координат. Если центр окружности совпадает с началом координат, ее уравнение принимает более простой вид: 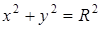 .
.
Ответ. 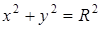 .
.
Задача 5.4. Дано полярное уравнение линии 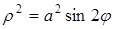 . Построить эту линию по точкам, задавая углу
. Построить эту линию по точкам, задавая углу 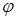 значения через промежуток
значения через промежуток 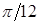 . Найти ее уравнение в декартовой системе координат.
. Найти ее уравнение в декартовой системе координат.
Решение. Поскольку левая часть данного уравнения неотрицательна, то угол 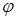 может изменяться только в тех пределах, для которых
может изменяться только в тех пределах, для которых 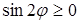 , т.е.
, т.е. 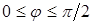 и
и 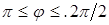 . Для вычисления значений
. Для вычисления значений 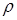 составим табл.
составим табл. 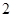 .
.
Таблица 2
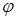 |
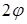 |
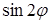 |
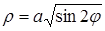 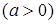 |
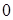 |
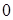 |
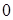 |
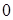 |
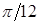 |
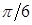 |
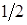 |
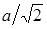 |
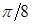 |
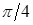 |
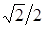 |
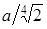 |
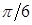 |
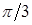 |
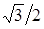 |
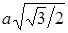 |
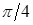 |
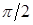 |
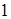 |
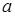 |
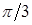 |
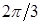 |
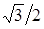 |
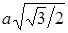 |
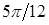 |
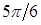 |
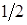 |
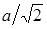 |
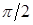 |
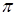 |
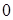 |
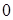 |
При изменении угла 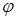 в пределах третьей, координатной четверти
в пределах третьей, координатной четверти 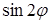 принимает те же значения, что и в первой координатной четверти. Поэтому линия будет расположена симметрично относительно начала координат. Для ее построения проведем из полюса лучи, соответствующие выбранным значениям
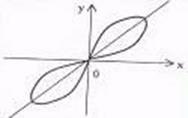
принимает те же значения, что и в первой координатной четверти. Поэтому линия будет расположена симметрично относительно начала координат. Для ее построения проведем из полюса лучи, соответствующие выбранным значениям 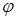 , и на каждом луче отложим вычисленные значения полярного радиуса. Полученные точки соединим плавной кривой (рис. 2.29). Построенная линия носит название лемнискаты Бернулли. Найдем ее уравнение в декартовой системе координат. Для этого воспользуемся формулой
, и на каждом луче отложим вычисленные значения полярного радиуса. Полученные точки соединим плавной кривой (рис. 2.29). Построенная линия носит название лемнискаты Бернулли. Найдем ее уравнение в декартовой системе координат. Для этого воспользуемся формулой 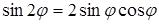 и подставим ее в уравнение линии
и подставим ее в уравнение линии
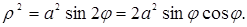
Теперь применим формулы (5.1) и (5.2), получим:
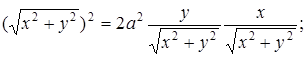
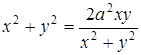 .
.
Окончательно имеем 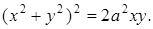
 |
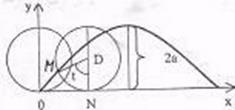 |
Рис. 2.29 Рис. 2.30
Задача 5.5. Записать параметрические уравнение циклоиды.
Решение. Циклоидой называется линия, описываемая точкой окружности, катящейся без скольжения по прямой линии.
Если оси координат расположить так, как показано на рис. 2.30, а за параметр 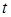 принять угол
принять угол 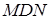 , то параметрические уравнения циклоиды запишутся в следующем виде:
, то параметрические уравнения циклоиды запишутся в следующем виде:
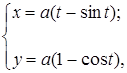
где 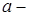 радиус катящейся окружности.
радиус катящейся окружности.
При изменение 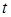 от
от 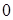 до
до 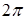 точка
точка 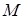 опишет одну арку циклоиды. При изменении
опишет одну арку циклоиды. При изменении 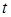 от
от 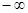 до
до 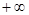 получается кривая, состоящая из бесконечного множества таких дуг, как изображенная на рис. 2.30.
получается кривая, состоящая из бесконечного множества таких дуг, как изображенная на рис. 2.30.
Дата добавления: 2017-09-01; просмотров: 3256;











