Примеры решение задач. Найти полуоси, координаты фокусов и эксцентриситет эллипса
Задача 6.1. Найти полуоси, координаты фокусов и эксцентриситет эллипса 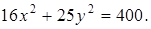
Решение. Разделив данное уравнение эллипса на 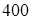 , приведем его к виду
, приведем его к виду 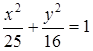 . Отсюда следует, что большая полуось эллипса
. Отсюда следует, что большая полуось эллипса 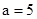 , а малая полуось
, а малая полуось 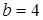 . Известно, что
. Известно, что 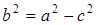 , поэтому
, поэтому
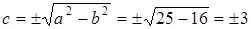 .
.
Следовательно, координаты фокусов 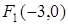 и
и 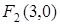 , а его эксцентриситет
, а его эксцентриситет 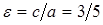 .
.
Ответ. 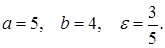
Задача 6.2. Эллипс касается оси ординат в начале координат, а центр симметрии его находится в точке 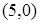 . Составить уравнение эллипса, если его эксцентриситет равен
. Составить уравнение эллипса, если его эксцентриситет равен 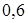 .
.
Решение. Выполним чертеж (рис. 2.35).
Каноническое уравнение такого эллипса 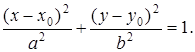 В нашем случае В нашем случае 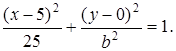 |
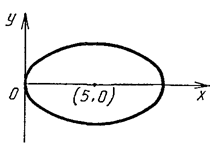 Рис. 2.35 Рис. 2.35 |
Известно, что 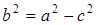 . Следовательно, для нахождения
. Следовательно, для нахождения 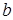 надо знать
надо знать 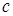 . Найдем
. Найдем 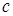 из формулы эксцентриситета:
из формулы эксцентриситета: 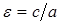 ,
, 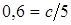 , откуда
, откуда 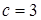 . Значит,
. Значит, 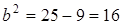 ,
, 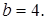
Итак, уравнение искомого эллипса
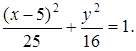
Ответ. 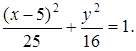
Задача 6.3. Определитель траекторию точки 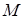 , которая при своем движении остается втрое ближе к точке
, которая при своем движении остается втрое ближе к точке 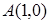 , чем к прямой
, чем к прямой 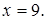
Решение. Траекторию точки 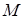 найдем как уравнение множества точек плоскости, обладающих свойством найдем как уравнение множества точек плоскости, обладающих свойством 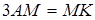 (рис. 2.36). Расстояние между любыми точками (рис. 2.36). Расстояние между любыми точками 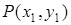 и и 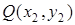 найдем по формуле найдем по формуле 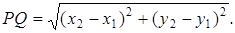 Следовательно, Следовательно, 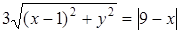 . . |
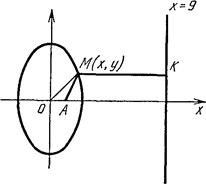 Рис. 2.36 Рис. 2.36 |
После преобразований получаем искомое уравнение:
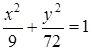 .
.
Таким образом, точка 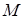 движется по эллипсу. При этом большая ось эллипса и его фокусы расположены на оси
движется по эллипсу. При этом большая ось эллипса и его фокусы расположены на оси 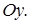
Ответ. 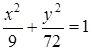 .
.
Задача 6.4.Действительная полуось гиперболы 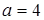 , эксцентриситет
, эксцентриситет 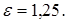 Составить каноническое уравнение гиперболы и начертить ее.
Составить каноническое уравнение гиперболы и начертить ее.
Решение. Эксцентриситет гиперболы 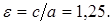 Следовательно,
Следовательно,
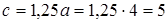 ,
, 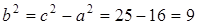 ,
,
откуда фокусы гиперболы 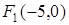 ,
, 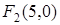 , а мнимая полуось
, а мнимая полуось 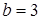 . Искомым уравнением гиперболы будет
. Искомым уравнением гиперболы будет
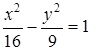 .
.
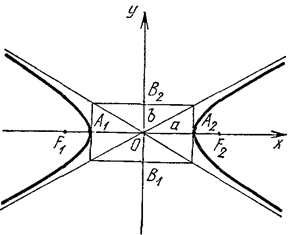 Рис. 2.37 Рис. 2.37 |
Вершины гиперболы: 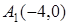 , , 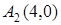 , , 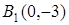 , , 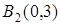 . Через них проводим стороны основного прямоугольника. Его диагонали . Через них проводим стороны основного прямоугольника. Его диагонали 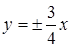 являются асимптотами гиперболы. Построим их. Затем через вершины являются асимптотами гиперболы. Построим их. Затем через вершины 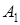 и и 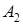 гиперболы проводим ее ветви, приближая их к асимптотам (рис. 2.37). гиперболы проводим ее ветви, приближая их к асимптотам (рис. 2.37). |
Ответ. 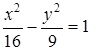 .
.
Задача 6.5.Дана равносторонняя гипербола 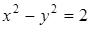 . Найти уравнение эллипса, фокусы которого находятся в фокусах гиперболы, если известно, что эллипс проходит через точку
. Найти уравнение эллипса, фокусы которого находятся в фокусах гиперболы, если известно, что эллипс проходит через точку 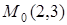 .
.
Решение. Для данной гиперболы 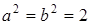 . Следовательно, из соотношения
. Следовательно, из соотношения 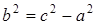 получаем
получаем 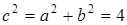 , откуда
, откуда 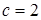 . Значит, фокусы гиперболы
. Значит, фокусы гиперболы 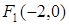 и
и 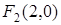 . В этих же точках находятся фокусы эллипса.
. В этих же точках находятся фокусы эллипса.
Обозначим через 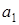 и
и 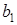 соответственно большую и малую полуоси эллипса. Тогда при условии, что
соответственно большую и малую полуоси эллипса. Тогда при условии, что 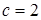 , будем иметь
, будем иметь 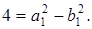 Для определения
Для определения 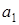 и
и 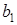 используем еще одно условие: что точка
используем еще одно условие: что точка 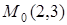 лежит на эллипсе, т.е. ее координаты должны удовлетворять уравнению эллипса
лежит на эллипсе, т.е. ее координаты должны удовлетворять уравнению эллипса
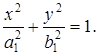 (6.8)
(6.8)
Это значит, что 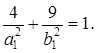 Таким образом, для определения
Таким образом, для определения 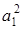 и
и 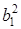 имеем систему уравнений
имеем систему уравнений
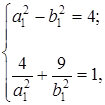
решив которую, получим 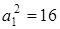 ,
, 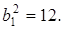 Подставив эти значения в уравнение (6.8), найдем
Подставив эти значения в уравнение (6.8), найдем
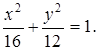
Ответ. 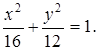
Задача 6.6. Асимптоты гиперболы имеют уравнения 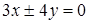 . Фокусы лежат на оси
. Фокусы лежат на оси 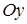 и расстояние между ними равно
и расстояние между ними равно 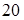 . Написать каноническое уравнение гиперболы и начертить ее.
. Написать каноническое уравнение гиперболы и начертить ее.
Решение. Так как фокусы гиперболы лежат на оси 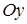 , то ее каноническое уравнение имеет вид
, то ее каноническое уравнение имеет вид
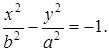
Разрешив уравнение асимптот относительно 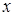 , получим
, получим 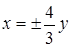 , откуда
, откуда 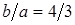 . Кроме того,
. Кроме того, 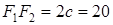 , т.е.
, т.е. 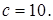 Так как для гиперболы
Так как для гиперболы 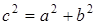 , то для нахождения
, то для нахождения 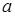 и
и 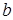 получим систему уравнений
получим систему уравнений
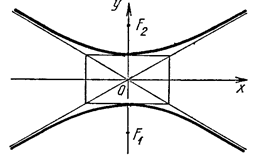 Рис. 2.38 Рис. 2.38 |
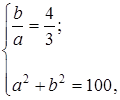 решив которую, будем иметь решив которую, будем иметь 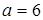 , , 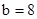 . Следовательно, каноническое уравнение гиперболы (рис. 2.38) . Следовательно, каноническое уравнение гиперболы (рис. 2.38) |
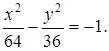
Ответ. 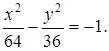
Задача 6.7. Составить уравнение параболы и ее директрисы, если парабола проходит через точки пересечения прямой 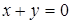 и окружности
и окружности 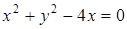 и симметрична относительно оси
и симметрична относительно оси 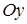 .
.
Решение. Найдем точки пересечения заданных линий, решив совместно их уравнения:
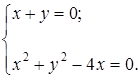
В результате получим два решения 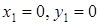 и
и 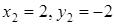 . Точки пересечения
. Точки пересечения 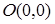 и
и 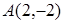 . Так как парабола проходит через точку
. Так как парабола проходит через точку 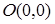 и симметрична относительно оси
и симметрична относительно оси 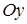 , то в этой точке будет находиться вершина параболы. Поэтому уравнение параболы имеет вид
, то в этой точке будет находиться вершина параболы. Поэтому уравнение параболы имеет вид 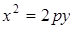 . Так как парабола проходит через точку
. Так как парабола проходит через точку 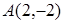 , то координаты этой точки удовлетворяют уравнению параболы:
, то координаты этой точки удовлетворяют уравнению параболы: 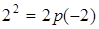 ,
, 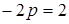 ,
, 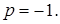
Итак, уравнением параболы будет 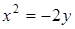 , уравнение директрисы
, уравнение директрисы 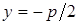 или
или 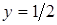 , откуда
, откуда 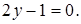
Ответ. 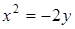 ;
; 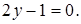
Задача 6.8. Мостовая арка имеет форму параболы. Определить параметр 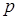 этой параболы, зная, что пролет арки равен
этой параболы, зная, что пролет арки равен 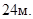 , а высота
, а высота 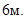
Решение.выберем прямоугольную систему координат так, чтобы вершина параболы (мостовой арки) находилась в начале координат, а ось симметрии совпадала с отрицательным направлением оси 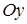 . В таком случае каноническое уравнение параболы имеет вид
. В таком случае каноническое уравнение параболы имеет вид 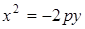 , а концы хорды арки
, а концы хорды арки 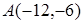 и
и 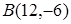 . Подставив координаты одного из концов хорды (например,
. Подставив координаты одного из концов хорды (например, 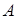 ) в уравнение параболы и решив полученное уравнение относительно
) в уравнение параболы и решив полученное уравнение относительно 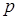 , получим
, получим 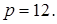
Ответ. 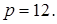
Задача 6.9. Привести уравнение кривой 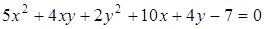 к каноническому виду и построить эту кривую.
к каноническому виду и построить эту кривую.
Решение. В уравнении 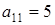 ,
, 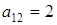 ,
, 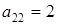 ,
, 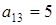 ,
, 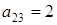 ,
, 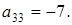 Вычислим дискриминант старших членов:
Вычислим дискриминант старших членов:
 .
.
Так как 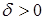 , данная линия является кривой эллиптического типа.
, данная линия является кривой эллиптического типа.
Найдем центр кривой из системы
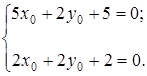
Решив ее, получим 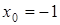 ,
,  .
.
С помощью параллельного переноса осей координат в центр 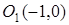 уравнение кривой в новой системе
уравнение кривой в новой системе 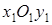 приводится к виду:
приводится к виду:
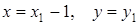 ,
,
подставив в исходное уравнение кривой, получим
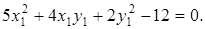 (6.9)
(6.9)
Для дальнейшего упрощения уравнения (6.9) применим правило приведения квадратичной формы к каноническому виду. Составим характеристическое уравнение
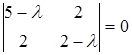 или
или 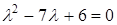 .
.
Отсюда 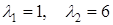 .
.
Повернув теперь оси координат так, чтобы направления осей 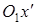 и
и 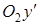 совпадали с главными направлениями квадратичной формы, уравнение (6.5) приведем к каноническому виду
совпадали с главными направлениями квадратичной формы, уравнение (6.5) приведем к каноническому виду
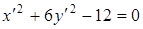 или
или 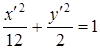 .
.
Из уравнения видно, что это эллипс с полуосями 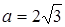 ,
, 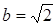 . Чтобы построить этот эллипс найдем главное направление, соответствующее характеристическому числу
. Чтобы построить этот эллипс найдем главное направление, соответствующее характеристическому числу 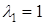 (его мы приняли за ось
(его мы приняли за ось 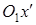 в каноническом уравнении). Подставив коэффициенты нашего уравнения в систему
в каноническом уравнении). Подставив коэффициенты нашего уравнения в систему
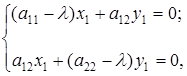
получим
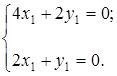
Полагая 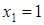 , находим, что
, находим, что 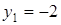 . Единичный вектор
. Единичный вектор 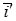 оси
оси 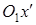 имеет в системе
имеет в системе 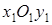 координаты
координаты 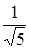 и
и 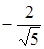 . Следовательно,
. Следовательно, 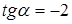 , а
, а 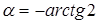 .
.
Повернув систему 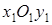 на угол на угол 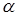 по часовой стрелке, получим прямоугольную систему координат по часовой стрелке, получим прямоугольную систему координат 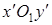 , в которой легко построить эллипс (рис. 3.39). Задача 6.10. Преобразовать к каноническому виду уравнение , в которой легко построить эллипс (рис. 3.39). Задача 6.10. Преобразовать к каноническому виду уравнение 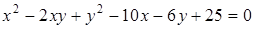 (6.10) и построить линию, задаваемую этим уравнением. (6.10) и построить линию, задаваемую этим уравнением. |
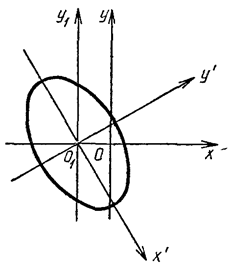 Рис. 3.39 Рис. 3.39 |
Решение. В исходном уравнении 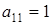 ,
, 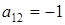 ,
, 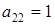 ,
, 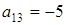 ,
, 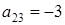 ,
, 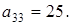 Дискриминант старших членов
Дискриминант старших членов
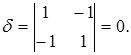
Следовательно, уравнение определяет нецентральную линию второго порядка, т.е. линию параболического типа.
Составим характеристическое уравнение квадратичной формы старших членов:
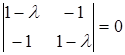 или
или 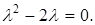
Отсюда 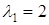 ,
, 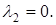
Найдем главное направление, соответствующее характеристическому числу 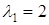 . Для этого подставим в систему
. Для этого подставим в систему
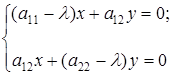
коэффициенты нашего уравнения. Получим
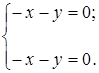
Полагая 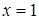 , имеем
, имеем 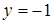 . Следовательно, главное направление, соответствующее характеристическому числу
. Следовательно, главное направление, соответствующее характеристическому числу 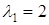 , определяется вектором
, определяется вектором 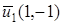 . Нормируя его, находим единичный вектор:
. Нормируя его, находим единичный вектор: 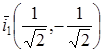 . Это значит, что
. Это значит, что 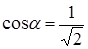 , а
, а 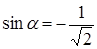 , т.е. поворачиваем систему
, т.е. поворачиваем систему 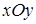 на угол
на угол 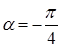 .
.
Используя теперь равенства (6.10), имеем:
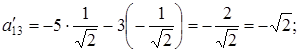

Следовательно, уравнение (10.17) в системе координат 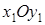 принимает вид
принимает вид
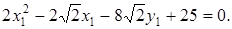 (6.11)
(6.11)
Уравнение (6.11) определяет параболу. Для приведения его к каноническому виду найдем координаты нового начала. Сгруппируем члены с одинаковыми переменными и выделим полный квадрат:
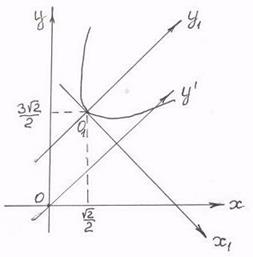 Рис. 2.40 Рис. 2.40 |
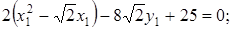 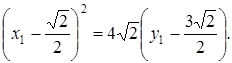 После параллельного переноса осей координат в новое начало После параллельного переноса осей координат в новое начало 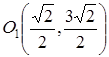 уравнение параболы (6.11) в системе координат уравнение параболы (6.11) в системе координат 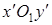 примет канонический вид примет канонический вид 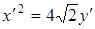 . Расположение параболы показано на рис. 2.40. . Расположение параболы показано на рис. 2.40. |
Дата добавления: 2017-09-01; просмотров: 5416;











