Циркуляция вектора напряжённости электростатического поля.

Рассмотрим некоторые следствия из установленного принципа.

Если 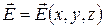- произвольное электростатическое поле, 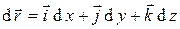- направленный отрезок контура 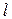, то работу электростатического поля по бесконечно медленному перемещению положительного единичного точечного заряда можно описать с помощью криволинейного интеграла

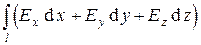. (1)

Циркуляцией вектора 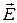по замкнутому контуру называют скалярную величину

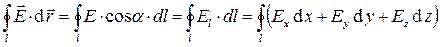. (2)

Здесь угол 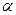- угол между направлением вектора 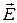и направленным элементарным отрезком контура 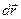, 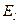- проекция вектора 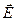на направление 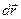, величина 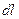является модулем элементарного направленного отрезка контура 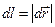. В определение циркуляции обязательно входит указание направления обхода контура. Очевидно, что изменение направления обхода приводит к смене алгебраического знака циркуляции. Заметим, что формальное определение понятия «циркуляция векторного поля» (2) не связано с физическим перемещением заряда по траектории: в нестационарном случае величина циркуляции рассчитывается для фиксированного момента времени, одного и того же для всех точек контура. При описании реального движения заряда пришлось бы учитывать, что вместе с изменением положения заряда изменялось бы и время наблюдения. В этой связи полезно помнить высказывание нобелевского лауреата по физике Р. Фейнмана о том, что абстрактное математическое представление зачастую оказывается и самым полным и самым правильным и самым содержательным.

Специального общепринятого символьного обозначения для циркуляции векторного поля не существует, а содержание понятия становится ясным из рассмотрения выражения

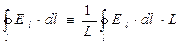, (3)

где 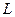- длина контура 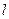. Теперь можно сформулировать интуитивное определение циркуляции векторного поля по замкнутому контуру конечной длины: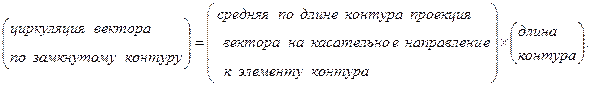

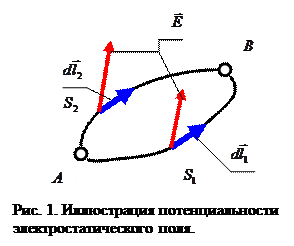В силу установленного выше принципа потенциальности электростатического поля выражение (2) должно обращаться в нуль для любого замкнутого контура :

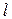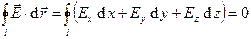. (4)

Условие (4) играет важную роль в электростатике: в реально существующем электростатическом поле обязательно выполнено интегральное условие потенциальности (4).

Обратим внимание читателя на то, что из условия (4) следует важный физический результат: силовые линии напряжённости электростатического поля не могут быть замкнутыми и не могут пересекаться, в противном случае условие (4) было бы несправедливо. Силовые линии или «замыкаются» на электрический заряд, или уходят «на бесконечность». В связи со сказанным следует отметить, что выбранное положительное направление вдоль силовой линии не может измениться на противоположное ни в одной точке пространства, через которую проходит рассматриваемая силовая линия.

Рассмотрим перемещение единичного положительного сосредоточенного электрического заряда из произвольной точки пространства А в произвольную точку В по двум произвольным траекториям 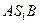и 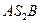(рис.1). Справедливо утверждение, что

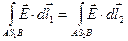. (5)

Действительно, если перенести упомянутый электрический заряд по замкнутому контуру 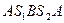, то получим в итоге нуль в силу результата (4). Но интеграл по траектории 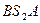только знаком отличается от интеграла по траектории 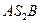, поэтому

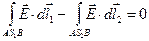
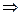
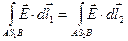. (6)

Таким образом, ещё раз получена вторая, эквивалентная первой, формулировка свойства потенциальности электростатического поля. Заметим, что и условие потенциальности электростатического поля (4) и полученное условие (6) записаны в интегральной форме.